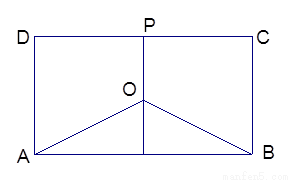
某地有三家工厂，分别位于矩形ABCD 的顶点A,B 及CD的中点P 处，已知AB=20km,CB =10km ，为了处理三家工厂的污水，现要在矩形ABCD 的区域中（含边界），且与A,B等距离的一点O 处建造一个污水处理厂，并铺设排污管道AO,BO,OP ，设排污管道的总长为km．

   （Ⅰ）设∠BAO=(rad)，将表示成的函数关系式；

  

（Ⅱ）请用（Ⅰ）中的函数关系式，确定污水处理厂的位置，使三条排污管道总长度最短．

 

 

 

某社区的常住人口中，有成年人3200人，其中有无业人员1000人，从事个体劳动的有1160人，有固定收入的上班人员1040人，如果想通过调查其中160人的生活消费情况来了解本社区群众的生活消费情况，考虑到由于各种人员情况的差异，而同一阶层人员的差异较小，问应当采取怎样的抽取方法？从事个体劳动的人员中应抽查多少人？在本问题的设计中还有哪些重要因素将影响调查效果？应怎样改进抽查方案使效果更加客观？

 

(1)假设某地区有高中生2 400人，初中生10 900人，小学生11 000人，此地教育部门为了了解本地区中小学的近视情况及其形成原因，要从本地区的小学生中抽取1%的学生进行调查，你认为应当怎样抽取样本？

(2)想一想为什么这样取各个学段的个体数？

(3)请归纳分层抽样的定义.

(4)请归纳分层抽样的步骤.

(5)分层抽样时如何分层？其适用于什么样的总体？

（本小题10分）

某餐厅供应客饭，每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种，现在餐厅准备了五种不同的荤菜，若要保证每位顾客有200种以上不同选择，则餐厅至少还需准备多少不同的素菜品种？（要求写出必要的解答过程）