
题目列表(包括答案和解析)
次数 同学 |
一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
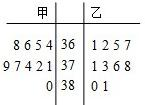
| 甲 | 90 | 50 | 70 | 80 | 70 | 60 | 80 | 60 | 70 | 70 |
| 乙 | 20 | 40 | 60 | 80 | 70 | 70 | 80 | 90 | 90 | 100 |
 某学校问了预防甲流感,每天都对同学进行体温抽查,某一天,随机抽取甲,乙两个班级各10名同学,测量他们的体温如下图(单位0.1摄氏度)
某学校问了预防甲流感,每天都对同学进行体温抽查,某一天,随机抽取甲,乙两个班级各10名同学,测量他们的体温如下图(单位0.1摄氏度)(满分12分)甲、乙两名同学在高一学年中(相同条件下)都参加数学考试十次,每次考试成绩如下表:
|
同学 |
一 |
二 |
三 |
四 |
五 |
六 |
七 |
八 |
九 |
十 |
|
甲 |
90 |
50 |
70 |
80 |
70 |
60 |
80 |
60 |
70 |
70 |
|
乙 |
20 |
40 |
60 |
80 |
70 |
70 |
80 |
90 |
90 |
100 |
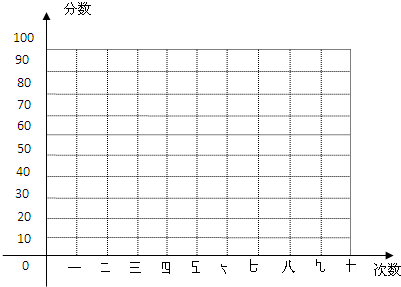
请在坐标系中画出甲、乙两同学的成绩折线图,并从以下不同角度对这次测试结果进行分析。
(1)从平均数和方差相结合看,分析谁的成绩更稳定些;
(2)从平均数和中位数相结合看,分析谁的成绩好些;
(3)从平均数和成绩为90分以上的次数相结合看,分析谁的成绩好些 ;
(4)从折线图上两人成绩分数的走势看,分析谁更有潜力。
在某次知识抢答赛的预赛中,甲乙两位同学分在同一小组,主持人给每个小组出四个必答题,每次只可由一位选手作答,每个小组只有答对不少于三道题才有资格进入决赛。已知对每道题,甲同学回答正确的概率为![]() ,乙同学回答正确的概率为
,乙同学回答正确的概率为![]() .比赛规则规定可任选一位同学答第一题,如果回答正确,则仍由他继续回答下一题,如果答错,则下一题由另一位同学回答。每个同学答题行为是相互独立的。甲乙两人决定先由甲回答第一题.
.比赛规则规定可任选一位同学答第一题,如果回答正确,则仍由他继续回答下一题,如果答错,则下一题由另一位同学回答。每个同学答题行为是相互独立的。甲乙两人决定先由甲回答第一题.
(1)以X表示甲乙两同学所在小组答对题目的个数,求X的分布列;
(2)甲乙两同学所在小组晋级决赛的概率是多少?
学校为了预防甲流感,每天上午都要对同学进行体温抽查。某一天,随机抽取甲、乙两个班级各10名同学,测量他们的体温如图:(单位0.1℃)

(1)哪个班所选取的这10名同学的平均体温高?
(2)一般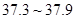 ℃为低热,
℃为低热,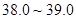 ℃为中等热,
℃为中等热,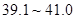 ℃为高热。按此规定,记事件A为“从甲班发热的同学中任选两人,有中等热的同学”,记事件B为“从乙班发热的同学中任选两人,有中等热的同学”,分别求事件A和事件B的概率.
℃为高热。按此规定,记事件A为“从甲班发热的同学中任选两人,有中等热的同学”,记事件B为“从乙班发热的同学中任选两人,有中等热的同学”,分别求事件A和事件B的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com