
题目列表(包括答案和解析)
(本小题满分12分)
已知等差数列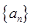 满足
满足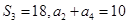 。
。
(Ⅰ)求通项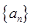 的通项公式及
的通项公式及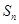 的最大值;
的最大值;
(Ⅱ)设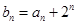 ,求数列
,求数列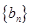 的其前
的其前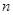 项和
项和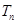 .
.
(本题满分12分)已知数列![]() 中,
中,![]() ,前
,前![]() 项和
项和![]() 与通项
与通项![]() 满足
满足![]() ,求通项
,求通项![]() 的表达式.
的表达式.
已知函数 ,数列
,数列 的项满足:
的项满足: ,(1)试求
,(1)试求
(2) 猜想数列 的通项,并利用数学归纳法证明.
的通项,并利用数学归纳法证明.
【解析】第一问中,利用递推关系 ,
, 
 ,
, 
第二问中,由(1)猜想得: 然后再用数学归纳法分为两步骤证明即可。
然后再用数学归纳法分为两步骤证明即可。
解: (1)  ,
,

 ,
,  …………….7分
…………….7分
(2)由(1)猜想得:
(数学归纳法证明)i)  ,
,
 ,命题成立
,命题成立
ii) 假设 时,
时, 成立
成立
则 时,
时,


综合i),ii) :  成立
成立
口袋里装有大小相同的4个红球和8个白球,甲、乙两人依规则从袋中有放回摸球,每次摸出一个球,规则如下:若一方摸出一个红球,则此人继续下一次摸球;若一方摸出一个白球,则由对方接替下一次摸球,且每次摸球彼此相互独立,并由甲进行第一次摸球。
(I)求在前三次摸球中,甲摸得红球的次数ξ的数学期望。
(II)设第n次由甲摸球的概率为![]() 的递推关系,并求数列
的递推关系,并求数列![]() 的通项公式。
的通项公式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com