
题目列表(包括答案和解析)
已知数列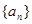 满足
满足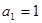 ,
,
(1)求证:数列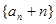 是等比数列;
是等比数列;
(2)求数列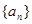 的通项和前n项和
的通项和前n项和 .
.
【解析】第一问中,利用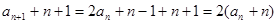 ,得到
,得到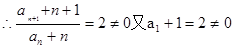 从而得证
从而得证
第二问中,利用∴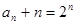 ∴
∴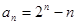 分组求和法得到结论。
分组求和法得到结论。
解:(1)由题得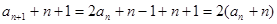 ………4分
………4分
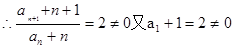 ……………………5分
……………………5分
∴数列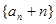 是以2为公比,2为首项的等比数列;
……………………6分
是以2为公比,2为首项的等比数列;
……………………6分
(2)∴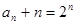 ……………………8分
……………………8分
∴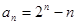 ……………………9分
……………………9分
∴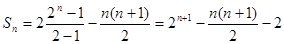
| n(a1+an) |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n( a1+an) | 2 |
| ||
| n个1 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com