
题目列表(包括答案和解析)
(08年黄冈中学一模理) (本小题满分13分)过抛物线![]() 的焦点F作直线l与抛物线交于A、B.
的焦点F作直线l与抛物线交于A、B.
(1)求证:![]() 不是直角三角形;
不是直角三角形;
(2)当l的斜率为![]() 时,抛物线上是否存在点C,使
时,抛物线上是否存在点C,使![]() 为直角三角形且B为直角(点B位于x轴下方)?若存在,求出所有的点C;若不存在,说明理由.
为直角三角形且B为直角(点B位于x轴下方)?若存在,求出所有的点C;若不存在,说明理由.
(08年湖北卷理)(本小题满分12分)
水库的蓄水量随时间而变化,现用t表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为
V(t)=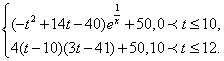
(Ⅰ)该水库的蓄求量小于50的时期称为枯水期.以i-1<t<t表示第1月份(i=1,2,…,12),同一年内哪几个月份是枯水期?
(Ⅱ)求一年内该水库的最大蓄水量(取e=2.7计算)
(08年安徽皖南八校联考理)(本小题满分14分)
数列![]() 的首项
的首项![]() =1,前
=1,前![]() 项和为
项和为![]() 满足
满足![]() (常数
(常数![]() ,
,![]() ).
).
(1)求证:数列![]() 是等比数列.
是等比数列.
(2)设数列![]() 的公比为
的公比为![]() ,作数列
,作数列![]() ,使
,使![]() ,
,![]() (
(![]() 2,3,
2,3,
4,…),求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,若存在
,若存在![]() ,且
,且![]() ;
;
使![]() (
(![]() …
…![]() )
)![]() ,试求
,试求![]() 的最小值.
的最小值.
(08年湖北卷理)(本小题满分14分)
已知数列{an}和{bn}满足:a1=λ,an+1=![]() 其中λ为实数,n为正整数.
其中λ为实数,n为正整数.
(Ⅰ)对任意实数λ,证明数列{an}不是等比数列;
(Ⅱ)试判断数列{bn}是否为等比数列,并证明你的结论;
(Ⅲ)设0<a<b,Sn为数列{bn}的前n项和.是否存在实数λ,使得对任意正整数n,都有
a<Sn<b?若存在,求λ的取值范围;若不存在,说明理由.
(09年长沙一中第八次月考理)(本小题满分12分)我校文化体育艺术节的乒乓球决赛在甲乙两人中进行,比赛规则如下:比赛采用7局4胜制(先胜4局这获胜即比赛结束),在每一局比赛中,先得11分的一方为胜方;比赛没有平局,10平后,先连得2分的一方为胜方![]()
(1)根据以往战况,每局比赛甲胜乙的概率为0.6,设比赛的场数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com