
题目列表(包括答案和解析)
(本题满分16分)
已知数列![]() 的首项为
的首项为![]() ,设
,设![]()
![]() .
.
(1)若![]() 为常数列,求
为常数列,求![]() 的值;
的值;
(2)若![]() 为公比为
为公比为![]() 的等比数列,求
的等比数列,求![]() 的解析式;
的解析式;
(3)数列![]() 能否成等差数列,使得
能否成等差数列,使得![]() 对一切
对一切![]() 都成立?若能,求出数列
都成立?若能,求出数列![]() 的通项公式;若不能,试说明理由.
的通项公式;若不能,试说明理由.
(本题满分16分)已知点(1,![]() )是函数
)是函数![]() 且
且![]() )的图象上一点,等比数列
)的图象上一点,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]()
![]() 的首项为
的首项为![]() ,且前
,且前![]() 项和
项和![]() 满足
满足![]() -
-![]() =
=![]() +
+![]() (
(![]() ).
).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若数列{![]() 前
前![]() 项和为
项和为![]() ,问
,问![]() >
>![]() 的最小正整数
的最小正整数![]() 是多少? .
是多少? . ![]()
![]()
(本题满分16分)
已知有穷数列 共有
共有 项(整数
项(整数 ),首项
),首项 ,设该数列的前
,设该数列的前 项和为
项和为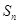 ,且
,且 其中常数
其中常数 ⑴求
⑴求 的通项公式;⑵若
的通项公式;⑵若 ,数列
,数列 满足
满足
求证: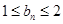 ;
;
⑶若⑵中数列 满足不等式:
满足不等式: ,求
,求 的最大值.
的最大值.
(本题满分16分)
已知有穷数列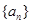 共有
共有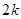 项(整数
项(整数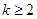 ),首项
),首项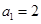 ,设该数列的前
,设该数列的前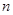 项和为
项和为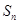 ,且
,且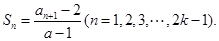 其中常数
其中常数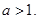 ⑴求
⑴求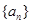 的通项公式;⑵若
的通项公式;⑵若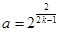 ,数列
,数列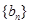 满足
满足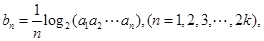
求证: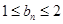 ;
;
⑶若⑵中数列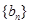 满足不等式:
满足不等式: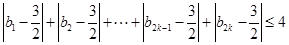 ,求
,求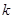 的最大值.
的最大值.
 共有
共有 项(整数
项(整数 ),首项
),首项 ,设该数列的前
,设该数列的前 项和为
项和为 ,且
,且 其中常数
其中常数 ⑴求
⑴求 的通项公式;⑵若
的通项公式;⑵若 ,数列
,数列 满足
满足
 ;
; 满足不等式:
满足不等式: ,求
,求 的最大值.
的最大值.一、填空题:
1.
 ,均有x 2+ x +1≥0 2.第一象限 3.充分而不必要条件 4. 0.01
,均有x 2+ x +1≥0 2.第一象限 3.充分而不必要条件 4. 0.01
5. 4 6. 2550 7.  8.①④ 9. R(S1+S2+S3+S4)
8.①④ 9. R(S1+S2+S3+S4)
10.
 ,11.
,11.  12.1
13.
12.1
13.
 14.
14. 
二、解答题:
15.(Ⅰ)因为各组的频率和等于1,故第四组的频率:

 3′
3′
直方图如右所示 6′



 (Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,频率和为
(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,频率和为  所以,抽样学生成绩的合格率是
所以,抽样学生成绩的合格率是 %.. 9 ′
%.. 9 ′
利用组中值估算抽样学生的平均分

=
 =71
=71
估计这次考试的平均分是71分 12′
16.(1)证明:连结BD.
在长方体 中,对角线
中,对角线 .
.
又 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,
 .
.
 .
.
又B1D1平面 ,
, 平面
平面 ,
,
 EF∥平面CB1D1. 6′
EF∥平面CB1D1. 6′
(2) 在长方体
在长方体 中,AA1⊥平面A1B
中,AA1⊥平面A1B
 AA1⊥B1D1.
AA1⊥B1D1.
又 在正方形A1B
在正方形A1B
 B1D1⊥平面CAA
B1D1⊥平面CAA
又 B1D1平面CB1D1,
B1D1平面CB1D1,
 平面CAA
平面CAA
17. (1)由 得
得 4′
4′
由正弦定理得



 6′
6′
 8′
8′
(2)
= 10′
10′
= 12′
12′
由(1)得


 15′
15′
18.(1)设C:+=1(a>b>0),设c>0,c2=a2-b2,由条件知a-c=,=,
∴a=1,b=c=,
故C的方程为:y2+=1 5′
(2)由=λ,
∴λ+1=4,λ=3 或O点与P点重合= 7′
当O点与P点重合=时,m=0
当λ=3时,直线l与y轴相交,则斜率存在。
设l与椭圆C交点为A(x1,y1),B(x2,y2)
得(k2+2)x2+2kmx+(m2-1)=0
Δ=(
x1+x2=, x1x2= 11′
∵=3 ∴-x1=3x2 ∴
消去x2,得3(x1+x2)2+4x1x2=0,∴3()2+4=0
整理得4k
m2=时,上式不成立;m2≠时,k2=,
因λ=3 ∴k≠0 ∴k2=>0,∴-1<m<- 或 <m<1
容易验证k2>
即所求m的取值范围为(-1,-)∪(,1)∪{0} 16′
19. ⑴由题意得 4′
4′

 (n≥2),
(n≥2),
又∵ ,
,
 数列
数列 是以
是以 为首项,以2为公比的等比数列。 8′
为首项,以2为公比的等比数列。 8′
[则

 (
( )]
)]
⑵由 及
及 得
得

 ,
11′
,
11′
则
 13′
13′

 16′
16′
20. (1)设
 ∴
∴ ∴
∴
由
又∵ ∴
∴
∴ 6′
6′
于是
由 得
得 或
或 ; 由
; 由 得
得 或
或
故函数 的单调递增区间为
的单调递增区间为 和
和 ,
,
单调减区间为 和
和 10′
10′
(2)证明:据题意 且x1<x2<x3,
且x1<x2<x3,
由(1)知f (x1)>f (x2)>f (x3),

 14′
14′


即ㄓ 是钝角三角形.
18′
是钝角三角形.
18′
第Ⅱ部分 加试内容
一.必答题:
1.(1)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,由题意知 4′
4′
(2)ξ可取1,2,3,4.
 ,
,
 ; 8′
; 8′
故ξ的分布列为
ξ
1
2
3
4
P





答:ξ的数学期望为 10′
10′
2.(1)由 得
得 ,
,
求得 3′
3′
(2)猜想 5′
5′
证明:①当n=1时,猜想成立。 6′
②设当n=k时 时,猜想成立,即
时,猜想成立,即 , 7′
, 7′
则当n=k+1时,有 ,
,
所以当n=k+1时猜想也成立 9′
③综合①②,猜想对任何 都成立。
10′
都成立。
10′
二、选答题:
 3.(1)∵DE2=EF?EC,
3.(1)∵DE2=EF?EC,
∴DE : CE=EF: ED.
∵ÐDEF是公共角,
∴ΔDEF∽ΔCED. ∴ÐEDF=ÐC.
∵CD∥AP, ∴ÐC=Ð P.
∴ÐP=ÐEDF.----5′
(2)∵ÐP=ÐEDF, ÐDEF=ÐPEA,
∴ΔDEF∽ΔPEA. ∴DE : PE=EF : EA.即EF?EP=DE?EA.
∵弦AD、BC相交于点E,∴DE?EA=CE?EB.∴CE?EB=EF?EP. 10′
4.(矩阵与变换)
解:.
 ,
5′
,
5′
椭圆 在
在 的作用下的新曲线的方程为
的作用下的新曲线的方程为 10′
10′
5.(1)直线的参数方程为 ,即
,即 . 5′
. 5′
(2)把直线 代入
代入 ,
,
得 ,
, ,
,
则点 到
到 两点的距离之积为
两点的距离之积为 .
10′
.
10′
6.
 7′
7′
当且仅当 且
且
F有最小值 10′
10′
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com