
题目列表(包括答案和解析)
(06年江西卷理)如图,在四面体ABCD中,截面AEF经过四面体的内切球(与四个面都相切的球)球心O,且与BC,DC分别截于E、F,如果截面将四面体分成体积相等的两部分,设四棱锥A-BEFD与三棱锥A-EFC的表面积分别是S1,S2,则必有( )
A.S1<S2 B.S1>S

(08年江西卷文)连结球面上两点的线段称为球的弦.半径为4的球的两条弦![]() 的长度分别等于
的长度分别等于![]() 、
、![]() ,每条弦的两端都在球面上运动,则两弦中点之间距离的最大值为 .
,每条弦的两端都在球面上运动,则两弦中点之间距离的最大值为 .
(07年江西卷理)若![]() ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(06年江西卷理)(12分)
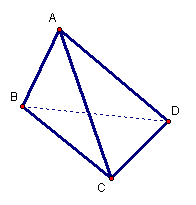
如图,在三棱锥A-BCD中,侧面ABD、ACD
是全等的直角三角形,AD是公共的斜边,
且AD=![]() ,BD=CD=1,另一个侧面是正三角形
,BD=CD=1,另一个侧面是正三角形
(1)求证:AD^BC
(2)求二面角B-AC-D的大小
(3)在直线AC上是否存在一点E,使ED与面BCD
成30°角?若存在,确定E的位置;若不存在,说明理由。
(07年江西卷)四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯,如图所示. 盛满酒后他们约定:先各自饮杯中酒的一半.设剩余酒的高度从左到右依次为![]() ,
,![]() ,
,![]() ,
,![]() ,则它们的大小关系正确的是( )
,则它们的大小关系正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com