
题目列表(包括答案和解析)
天文学上,太阳的半径、体积、质量和密度都是常用的物理量,利用小孔成像原理和万有引力定律相结合,可以简捷地估算出太阳的密度.假设地球上某处对太阳的张角为θ,如图所示.地球绕太阳公转的周期为T,太阳的密度为ρ,半径为R,质量为M,该处距太阳中心的距离为r,由于R与r间存在着三角关系,地球上该处物体绕太阳公转,由万有引力提供向心力,因此在θ已知的情况下,可方便地估算太阳密度.以一个长80cm的圆筒,在其一端封上厚纸,中间扎直径为1mm的孔,另一端封上一张画有同心圆的薄白纸,相邻同心圆的半径相差0.5mm,以此做标尺.把小孔对着太阳,筒壁与光线平行,另一端的薄白纸上可以看到一个圆光斑,这就是太阳的实像.光斑的半径r0=3.7mm.为了使观察效果明显,可在圆筒的观察端蒙上遮光布,形成暗室,如图所示.估算太阳的密度ρ=________kg/m3.(已知万有引力常量G=6.67×10-11N·m2/kg2)
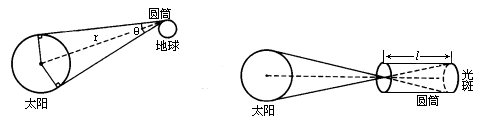
天文学上,太阳的半径、体积、质量和密度都是常用的物理量,利用小孔成像原理和万有引力定律相结合,可以简捷地估算出太阳的密度.假设地球上某处对太阳的张角为q ,如图1所示,地球绕太阳公转的周期为T,太阳的密度为r ,半径为R,质量为m,该处距太阳中心的距离为r,由于R与r间存在着三角关系,地球上该处物体绕太阳公转由万有引力提供向心力,因此,在q 已知的情况下,可方便地估算太阳的密度.
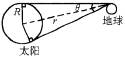
图1
以一个长为80cm的圆筒,在其一端封上厚纸,中间扎直径为1mm的圆孔,另一端封上一张画有同圆心的薄白纸,相邻同心圆的半径相差0.5mm,当作测量尺度,把小孔对着太阳,筒壁与光线平行,另一端的薄白纸上可以看到一个圆光斑,这就是太阳的实像,光斑的半径为r0=3.7mm,为了使观察效果明显,可在圆筒的观测端蒙上遮光布,形成暗室,如图2所示,利用小孔成像原理和万有引力定律,估算太阳的密度r =_________kg/m3.(已知万有引力常量G=6.67×10-11N·m2/kg2)
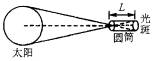
图2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com