
题目列表(包括答案和解析)
| OP |
| OQ |
| GD |
| GC |
| GE |
| GA |
| GF |
| GB |
| 1 |
| 2 |
| A |
| A |
| a |
| a |
| a |
| a |
| AB |
| a |
| A |
| AB |
| 1 |
| 3 |
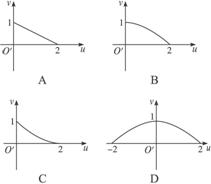
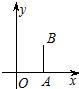 如图,在平面直角坐标系xOy中,A(1,0),B(1,1),映射f将xOy平面上的点P(x,y)对应到另一个平面直角坐标系uO′v上的点P′(2xy,x2-y2),例如xOy平面上的点P(2,1)在映射f的作用下对应到uO′v平面上的点P′(4,3),则当点P在线段AB上运动时,在映射f的作用下,动点P′的轨迹是( )
如图,在平面直角坐标系xOy中,A(1,0),B(1,1),映射f将xOy平面上的点P(x,y)对应到另一个平面直角坐标系uO′v上的点P′(2xy,x2-y2),例如xOy平面上的点P(2,1)在映射f的作用下对应到uO′v平面上的点P′(4,3),则当点P在线段AB上运动时,在映射f的作用下,动点P′的轨迹是( )A、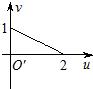 | B、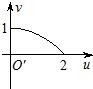 | C、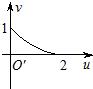 | D、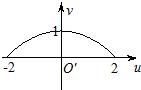 |

(1) 给定正整数n![]() 5,集合 An=
5,集合 An=![]() .是否存在一一映射
.是否存在一一映射 ![]() : An
: An![]() An满足条件:对一切k ( 1
An满足条件:对一切k ( 1![]() k
k ![]() n-1 ) , 都有k |
n-1 ) , 都有k | ![]() (1)+
(1)+![]() (2) +……+
(2) +……+![]() (k) ?
(k) ?
(2) N* 为全体正整数的集合,是否存在一一映射 ![]() : N*
: N*![]() N* 满足条件:对一切k
N* 满足条件:对一切k![]() N*, 都有k |
N*, 都有k | ![]() (1)+
(1)+![]() (2) + ……+
(2) + ……+![]() (k) ?
(k) ?
证明你的结论 .
注: 映射 ![]() : A
: A![]() B 称为一一映射,如果对任意 b
B 称为一一映射,如果对任意 b![]() B,有且只有一个 a
B,有且只有一个 a![]() A 使得
A 使得 ![]() (a)=b . 题中“|”为整除符号.
(a)=b . 题中“|”为整除符号.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com