
题目列表(包括答案和解析)
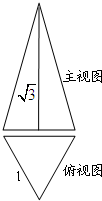 若正三棱锥的主视图与俯视图如图(单位cm),则左视图的面积为
若正三棱锥的主视图与俯视图如图(单位cm),则左视图的面积为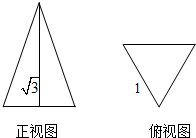 若正三棱锥的正视图与俯视图如图所视(单位:cm),则左视图的面积为( )
若正三棱锥的正视图与俯视图如图所视(单位:cm),则左视图的面积为( )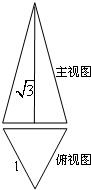
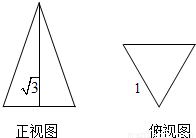
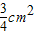
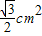
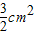
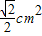
 若正三棱锥的主视图与俯视图如图(单位cm),则左视图的面积为 cm2.
若正三棱锥的主视图与俯视图如图(单位cm),则左视图的面积为 cm2.一、填空题
1.  ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ; 5.
; 5. ;
;
6. ;
7.
;
7. ; 8.3; 9.
; 8.3; 9. . 10.
. 10.
11. ; 12.
; 12. ; 13.
; 13. ; 14.
; 14. .
.
二、解答题
15.解:(1)由 得:
得:
 ,
,
由正弦定理知:  ,
,
(2) ,
,
由余弦定理知:
16.解:(Ⅰ)证明:取 的中点
的中点 ,连接
,连接
 因为
因为 是正三角形,
是正三角形,
所以
又 是正三棱柱,
是正三棱柱,
所以 面
面 ,所以
,所以
所以有 面
面
因为 面
面
所以 ;
;
(Ⅱ) 为
为 的三等分点,
的三等分点, .
.
连结 ,
, ,
,
∵  ,∴
,∴  .
.
∴  , ∴
, ∴ 
又∵ 面
面 ,
, 面
面
∴  平面
平面
17.解 (Ⅰ)设点P的坐标为(x,y),由P(x,y)在椭圆上,得


又由 知
知 ,
,
所以
(Ⅱ) 当 时,点(
时,点( ,0)和点(-
,0)和点(- ,0)在轨迹上.
,0)在轨迹上.
当 且
且 时,由
时,由 ,得
,得 .
.
又 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
在△QF ,所以有
,所以有
综上所述,点T的轨迹C的方程是
(Ⅲ) C上存在点M( )使S=
)使S= 的充要条件是
的充要条件是
由③得 ,由④得
,由④得 所以,当
所以,当 时,存在点M,使S=
时,存在点M,使S= ;
;
当 时,不存在满足条件的点M.
时,不存在满足条件的点M.
当 时,
时, ,
,
由 ,
,
 ,
,
 ,得
,得
18.解:(1) (或
(或 )(
)( )
)
(2)
当且仅当 ,即V=
,即V=
所以,博物馆支付总费用的最小值为7500元.
(3)解法1:由题意得不等式:
当保护罩为正四棱锥形状时, ,代入整理得:
,代入整理得: ,解得
,解得 ;
;
当保护罩为正四棱柱形状时, ,代入整理得:
,代入整理得: ,解得
,解得
又底面正方形面积最小不得少于 ,所以,底面正方形的面积最小可取
,所以,底面正方形的面积最小可取
解法2. 解方程 ,即
,即 得两个根为
得两个根为
由于函数 在
在 上递减,在
上递减,在 上递增,所以当
上递增,所以当 时,总费用超过8000元,所以V取得最小值
时,总费用超过8000元,所以V取得最小值
由于保护罩的高固定为 .所以当保护罩为正四棱柱时,保护罩底面积最小,
.所以当保护罩为正四棱柱时,保护罩底面积最小, m2
m2
又底面正方形面积最小不得少于 ,
, ,所以,底面正方形的面积最小可取
,所以,底面正方形的面积最小可取
19.解:(Ⅰ) 令
令 得
得
当 为增函数;
为增函数;
当 为减函数,
为减函数,
可知 有极大值为
有极大值为
(Ⅱ)欲使 在
在 上恒成立,只需
上恒成立,只需 在
在 上恒成立,
上恒成立,
设
 由(Ⅰ)知,
由(Ⅰ)知, ,
,

(Ⅲ) ,由上可知
,由上可知 在
在 上单调递增,
上单调递增,
 ①,
①,
同理 ②
②
两式相加得

20.解:(1)证明:因为
所以 即
即
可化为:
当且仅当 即
即 时
时
故
(2)因为

=

=

又由 可知
可知 =
=

即 =
=

解之得 
故得 所以
所以

因此 的通项公式为..
的通项公式为..
(3)解:


所以
即S的最大值为
三、附加题
∵ÐDEF是公共角,
∴ΔDEF∽ΔCED. ∴ÐEDF=ÐC.
∵CD∥AP, ∴ÐC=Ð P.
∴ÐP=ÐEDF.
(2)∵ÐP=ÐEDF, ÐDEF=ÐPEA,
∴ΔDEF∽ΔPEA. ∴DE : PE=EF : EA.即EF?EP=DE?EA.
∵弦AD、BC相交于点E,∴DE?EA=CE?EB.∴CE?EB=EF?EP.
21B.法一:特殊点法
在直线 上任取两点(2、1)和(3、3),…………1分
上任取两点(2、1)和(3、3),…………1分
则 ?
?
 即得点
即得点 …………3 分
…………3 分

 即得点
即得点
将 和
和 分别代入
分别代入 上得
上得

则矩阵 …………6 分
…………6 分
则 …………10 分
…………10 分
法二:通法
设 为直线
为直线 上任意一点其在M的作用下变为
上任意一点其在M的作用下变为 …………1分
…………1分
则
 …………3分
…………3分
代入 得:
得:
 其与
其与 完全一样得
完全一样得
则矩阵 …………6分
…………6分
则 …………10分
…………10分
 化为
化为 , ………4分
, ………4分
 ,
………6分
,
………6分
设动点P ,M
,M ,则
,则  , ………8分
, ………8分
又  ,得
,得 ;
………10分
;
………10分
法二:以极点为坐标原点建立直角坐标系,
将直线方程 化为
化为 ,………………4分
,………………4分
设P ,M
,M ,
, ,………6分
,………6分
又MPO三点共线, ,
, …………8分
…………8分
转化为极坐标方程 . ………10分
. ………10分
21D.证明: ∵a、b、c均为实数.
∴ (
( +
+ )≥
)≥ ≥
≥ ,当a=b时等号成立;
,当a=b时等号成立;
 (
( +
+ )≥
)≥ ≥
≥ ,当b=c时等号成立;
,当b=c时等号成立;
 (
( +
+ )≥
)≥ ≥
≥ .
.
三个不等式相加即得 +
+ +
+ ≥
≥ +
+ +
+ ,
,
当且仅当a=b=c时等号成立.
22.解:(I)以O为原点,OB,OC,OA分别为x,y,z轴建立空间直角坐标系.
则有A(0,0,1),B(2,0,0),C(0,2,0),E(0,1,0).
 cos<
cos< >
> .
.
由于异面直线BE与AC所成的角是锐角,故其余弦值是 .
.
 (II)
(II) ,
, ,
,
设平面ABE的法向量为 ,
,
则由 ,
, ,得
,得
取n=(1,2,2),
平面BEC的一个法向量为n2=(0,0,1),
 .
.
由于二面角A-BE-C的平面角是n1与n2的夹角的补角,其余弦值是- .
.
23.解: 的所有可能取值有6,2,1,-2;
的所有可能取值有6,2,1,-2; ,
,
 ,
,
故 的分布列为:
的分布列为:

6
2
1
-2

0.63
0.25
0.1
0.02
(2)
(3)设技术革新后的三等品率为 ,则此时1件产品的平均利润为
,则此时1件产品的平均利润为

依题意, ,即
,即 ,解得
,解得 所以三等品率最多为
所以三等品率最多为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com