
题目列表(包括答案和解析)
已知:对于给定的q∈N*及映射f:A→B,![]() .若集合
.若集合![]() ,且C中所有元素对应的象之和大于或等于q,则称C为集合A的好子集.
,且C中所有元素对应的象之和大于或等于q,则称C为集合A的好子集.
①对于q=2,A={a,b,c},映射f:x→1,x∈A,那么集合A的所有好子集的个数为________;
②对于给定的q,A={1,2,3,4,5,6,π},映射f:A→B的对应关系如下表:

若当且仅当C中含有π和至少A中2个整数或者C中至少含有A中5个整数时,C为集合A的好子集.写出所有满足条件的有序数组(q,y,z):________.
已知:对于给定的q∈N*及映射f:A→B,![]() .若集合
.若集合![]() ,且C中所有元素对应的象之和大于或等于q,则称C为集合A的好子集.
,且C中所有元素对应的象之和大于或等于q,则称C为集合A的好子集.
①对于q=2,A={a,b,c},映射f:x→1,x∈A,那么集合A的所有好子集的个数为________;
②对于给定的q,A={1,2,3,4,5,6,π},映射f:A→B的对应关系如下表:

若当且仅当C中含有π和至少A中2个整数或者C中至少含有A中5个整数时,C为集合A的好子集.写出所有满足条件的有序数组(q,y,z):________.
| x | 1 | 2 | 3 | 4 | 5 | 6 | π | ||||
| f(x) | 1 | 1 | 1 | 1 | 1 |
|
z |
| x | 1 | 2 | 3 | 4 | 5 | 6 | π | ||||
| f(x) | 1 | 1 | 1 | 1 | 1 |
|
z |
| x | 1 | 2 | 3 | 4 | 5 | 6 | π |
| f(x) | 1 | 1 | 1 | 1 | 1 | 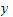 | z |
一、选择题:(本大题共8小题,每小题5分,共40分.)
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
答案
C
A
B
A
B
D
D
A
二、填空题(本大题共6小题,每小题5分.有两空的小题,第一空3分,第二空2分,共30分)
(9)1
(10)1,[0,1] (11)
(12) (13)(-2,
(13)(-2, ]∪[
]∪[ ,2)
(14)4,(5,1,3)
,2)
(14)4,(5,1,3)
三、解答题(本大题共6小题,共80分)
(15)(本小题共12分)
解:(Ⅰ)f
(x)=sin2x+2
 ………………………………………2分
………………………………………2分
=
=2sin(2x )………………………………………………………14分
)………………………………………………………14分
所以T= =
= .……………………………………………………………………5分
.……………………………………………………………………5分
由 +
+ ≤2x-
≤2x- ≤
≤ +
+ (k
(k Z)得
Z)得
 +
+ ≤x≤kπ+
≤x≤kπ+ (k
(k Z).…………………………………………………7分
Z).…………………………………………………7分
所以函数f (x)的最小正周期为 ,单调递减区间为[
,单调递减区间为[ ,
, ](k
](k Z).
Z).
(Ⅱ)由(Ⅰ)有f(x)=2sin(2x- ).
).
因为x
 ,
, ,
,
所以 .…………………………………………………………8分
.…………………………………………………………8分
因为sin( )=sin
)=sin <sin
<sin ,
,
所以当x= 时,函数f (x)取得最小值-
时,函数f (x)取得最小值- ;当x=
;当x= 时,函数f (x)取得最大值2.………………………………………………………………………………12分
时,函数f (x)取得最大值2.………………………………………………………………………………12分
(16)(本小题共12分)
解:(Ⅰ)因为f (x)=x2(x>0),所以g(x)= (x>0).
(x>0).
从而f ′(x)=2x,g′(x)= .…………………………………………3分
.…………………………………………3分
所以切线l1,l2的斜率分别为k1=f′(x0)=2x0,k2= g′(y0)=  .
.
又y0= ( x0>0),所以k2=
( x0>0),所以k2= .………………………………………4分
.………………………………………4分
因为两切线l1,l2平行,所以k1= k2. …………………………………5分
从而(2x0)2 =1.
因为x0>0.
所以x0=
所以M,N两点的坐标分别为( ,
, ),(
),( ,
, ).………………7分
).………………7分
(Ⅱ)设过O、M、N三点的圆的方程为:x2+y2+Dx+Ey+F=0.
因为圆过原点,所以F =0.因为M、N关于直线y =x对称,所以圆心在直线y=x
上.
所以D =E.………………………………………………………………………10分
又因为M ( ,
, )在圆上,
)在圆上,
所以D =E = .
.
所以过O、M、N三点的圆的方程为:x2+ y2  .………12分
.………12分
(17)(本小题共14分)
(Ⅰ)证明:连结AC1交A1C于点G,连结DG.
在正三棱柱ABC- A1B1 C1中,四边形ACC1A1是平行四边形,
∴AG=GC1.
 ∵AD=DB,
∵AD=DB,
∴DG∥BC1.………………………2分
∵DG 平面A1DC,BC1
平面A1DC,BC1 平面A1DC,
平面A1DC,
∴BC1∥平面A1DC.…………………4分
解法一:(Ⅱ)连结DC1,设C1到平面A1DC的距
离为h.
∵四边形ACC1A1是平行四边形,
∴S△ = S△
= S△ .
.
∴V =V
=V .
.
∵ S△ACD?AA1=
S△ACD?AA1= ,
,
∴ =
= .…………………………………………………………………………6分
.…………………………………………………………………………6分
在等边三角形ABC中,D为AB的中点,
∴CD = ,CD⊥AB.
,CD⊥AB.
∵AD是A1D在平面ABC内的射影,
∴CD⊥A1D.……………………………………………………………………………8分
∴S△ =
= …………………………………………………………………9分
…………………………………………………………………9分
∴h= ………………………………………………………………………9分
………………………………………………………………………9分
(Ⅲ)过点D作DE⊥AC交AC于E,过点D作DF⊥A1C交A1C于F,连结EF.
 ∵平面ABC⊥平面ACC1A1,DE
∵平面ABC⊥平面ACC1A1,DE 平面ABC,
平面ABC,
平面ABC∩平面ACC1A1=AC,
∴DE⊥平面ACC1A1.
∴EF是DF在平面ACC1A1内的射影.
∴EF⊥A1C.
∴∠DEF是二面角D-A1C-A的平面角.
……………………………………12分
在直角三角形ADC中,DE = =
= .
.
同理可求:DF=
∴sinDEF= .
.
∵∠DEF
 ,
,
∴∠DFE=arcsin .………………………………………………………………14分
.………………………………………………………………14分
解法二:过点A作AO⊥BC交BC于O,过点O作OE⊥BC交B1C1于E.因为平面
ABC⊥平面CBB1C1,所以AO⊥平面CBB1C1.分别以CB、OE、OA所在的直线为x
轴、y轴、z轴建立空间直角坐标系,如图所示.因为BC=1,AA1= ,△ABC是等
,△ABC是等
边三角形,所以O为BC的中点.则
O(0,0,0), ,
, ,
,

 ,
, ,
,
C1 ………………6分
………………6分
(Ⅱ)设平面A1DC的法向量为n=(x,y,z),
 则
则
∵ =(
=( ,0,
,0, ),
), =(
=( ,
, ,
, ),
),
∴
取x = ,得平面A1DC的一个法向量为n =(
,得平面A1DC的一个法向量为n =( ,1,-3).………………………………8分
,1,-3).………………………………8分
 ∴C1到平面A1DC的距离为: =
∴C1到平面A1DC的距离为: = .…………………………………10分
.…………………………………10分
(Ⅲ)同(Ⅱ)可求平面ACA1的一个法向量为n1=( ,0,-1).………………………12分
,0,-1).………………………12分
设二面角D-A1C-A的大小为θ,则cosθ=cos<n,n1>= =
= .
.
∵ (0,π),
(0,π),
∴ =arccos
=arccos .…………………………………………………………………14分(18)(本小题共14分)
.…………………………………………………………………14分(18)(本小题共14分)
解(Ⅰ)由已知得P1+P2+P3=1.
∵P2=P3,∴P1+2P2=1.
∵P1,P2是方程25x2-15x +a=0的两个根,
∴P1+P2 = .
.
∴P1= ,P2=P3=
,P2=P3= .…………………………………………………………3分
.…………………………………………………………3分
(Ⅱ)ξ的可能取值为0,100,200,300,400.…………………………………4分
P(ξ=0) = ×
× =
= ,
,
P(ξ=100) =2× ×
× =
= ,
,
P(ξ=200) =2× ×
× +
+ ×
× =
= ,
,
P(ξ=300) =2× ×
× =
= ,
,
P(ξ=400) =  ×
× =
= .……………………………………………………9分
.……………………………………………………9分
随机变量ξ的分布列为:
ξ
0
100
200
300
400
P





(Ⅲ)销售利润总和的平均值为………………………………………………………11分
Eξ=0× +100×
+100× +200×
+200× +300×
+300× +400×
+400× =240.
=240.
∴销售两台这种家用电器的利润总和的平均值为240元.……………………14分
注:只求出Eξ,没有说明平均值为240元,扣1分.
(19)(本小题共14分)
解:(Ⅰ)设动点P的坐标为(x,y),则直线PA,PB的斜率分别是 ,
, .
.
由条件得 ?
? =
= .………………………………………………3分
.………………………………………………3分
即 +y2 =1(x≠0).
+y2 =1(x≠0).
所以动点P的轨迹C的方程为 +y2 =1(x≠0).………………………5分
+y2 =1(x≠0).………………………5分
注:无x≠0扣1分.
(Ⅱ)设点M,N的坐标分别是(x1,y1),(x2,y2).
当直线l垂直于x轴时,x1= x2= -1,y1=-y2, =
= .
.
所以 =(x1-2,y1)=(-3,y1),
=(x1-2,y1)=(-3,y1), =(x2-2,y2)=(-3,-y1).
=(x2-2,y2)=(-3,-y1).
所以 ?
? =9-
=9- =
= .…………………………………………………7分
.…………………………………………………7分
当直线l不垂直于x轴时,设直线l的方程为y=k(x+1),
由 得(1+2k2)x2+4k2x+2k2-2=0.
得(1+2k2)x2+4k2x+2k2-2=0.
所以x1+x2= ,x1x2=
,x1x2= .………………………………………9分
.………………………………………9分
所以 ?
? =(x1-2)(x2-2)+y1y2= x1x2-2(x1+x2) +4+y1y2.
=(x1-2)(x2-2)+y1y2= x1x2-2(x1+x2) +4+y1y2.
因为y1=k (x1+1),y2=(x2+1),
所以 ?
? =(k2 +1)x1x2+(k2-2)(x1+x2)+k2+4=
=(k2 +1)x1x2+(k2-2)(x1+x2)+k2+4= -
- <
< .
.
综上所述 ?
? 的最大值是
的最大值是 .……………………………………11分
.……………………………………11分
因为S≤ tanMQN恒成立,
tanMQN恒成立,
即 |
| |?|
|?| |sinMQN≤
|sinMQN≤
 恒成立.
恒成立.
由于 ?
? =
=
 >0.
>0.
所以cosMQN>0.
所以 ?
? ≤2
≤2 恒成立.……………………………………………13分
恒成立.……………………………………………13分
所以 的最小值为
的最小值为 .……………………………………………………14分
.……………………………………………………14分
注:没有判断∠MQN为锐角,扣1分.
(20)(本小题共14分)
解:(Ⅰ){an}不是无界正数列,理由如下:………………………………………1分
取M=5,显然an=3+2sin(n)
≤5,不存在正整数n0满足 >5;………………2分
>5;………………2分
{bn}是无界正数列.理由如下:………………………………………………………3分
对任意的正数M,取n0为大于2M的一个偶数,有 >
> >M,所以
>M,所以
{bn}是无界正数列.…………………………………………………………………4分
(Ⅱ)存在满足题意的正整数k.理由如下:
当n≥3时,
因为
= ≥
≥ >
> ,
,
即取k=3,对于一切n≥k,有 <n
<n 成立.………………9分
成立.………………9分
注:k取大于或等于3的整数即可.
(Ⅲ)证明:因为数列{an}是单调递增的正数列,
所以
>
即 <n-1+
<n-1+ .
.
因为{an}是无界正数列,取M =2a1,由定义知存在正整数n1,使 >2a1,
>2a1,
所以 <n1
<n1 .
.
由定义可知{an}是无穷数列,考察数列 ,
, ,
, ,…,显然这仍是一个单调递增的无界正数列,同上理由可知存在正整数n2,使得
,…,显然这仍是一个单调递增的无界正数列,同上理由可知存在正整数n2,使得
 <(n2-n1)
<(n2-n1) .
.
重复上述操作,直到确定相应的正整数n4018.
则 <
<
= -2009.
-2009.
即存在正整数m= ,使得
,使得 <m-2009成立.
<m-2009成立.
…………………………………………………………………………………14分
说明:其他正确解法按相应步骤给分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com