[例1]已知向量的夹角为钝角,求m的取值范围. 解:夹角为钝角则 解得 又当时,, ∴m的取值范围是 [例2]已知两单位向量与的夹角为.若.试求与的夹角. 解:由题意.且与的夹角为 所以. . .同理可得 而.设为与的夹角.则 [例3]已知向量,,且满足关系 ,. (1)求证:; (2)求将表示为k的函数f(k). 的最小值及取最小值时的夹角θ. 解(1)证明: (2) (3) 当且仅当即k=1时,故f(x)的最小值是 此时 [例4]如图.四边形MNPQ是⊙C的内接梯形.C是圆心.C在MN上.向量与的夹角为120°.·=2. (1)求⊙C的方程, (2)求以M.N为焦点且过点P.Q的椭圆的方程. 剖析:需先建立直角坐标系.为了使所求方程简单.需以C为原点.MN所在直线为x轴.求⊙C的方程时.只要求半径即可.求椭圆的方程时.只需求a.b即可. 解:(1)以MN所在直线为x轴.C为原点.建立直角坐标系xOy. ∵与的夹角为120°.故∠QCM=60°.于是△QCM为正三角形.∠CQM=60°. 又·=2.即||||cos∠CQM=2.于是r=||=2. 故⊙C的方程为x2+y2=4. (2)依题意2c=4.2a=|QN|+|QM|. 而|QN|==2.|QM|=2. 于是a=+1.b2=a2-c2=2. ∴所求椭圆的方程为+=1. [研讨.欣赏]如图.△AOE和△BOE都是边长为1的等边三角形.延长OB到C使|BC|=t(t>0).连AC交BE于D点. ⑴用t表示向量和的坐标, ⑵求向量和的夹角的大小. 解:⑴=((t+1).-(t+1)). ∵=t.∴=t.=.又=(.). =-=(t.-(t+2)),∴=(.-). ∴=(.-) ⑵∵=(.-). ∴·=·+·= 又∵||·||=·= ∴cos<.>==.∴向量与的夹角为60° 【
查看更多】
题目列表(包括答案和解析)
已知向量
,
的夹角为60°,且
||=1,||=2,设
=3-,
=t+2(1)求
•; (2)试用t来表示
•的值;(3)若
与
的夹角为钝角,试求实数t的取值范围.
查看答案和解析>>
已知向量
,
的夹角为60°,且
||=1,||=2,设
=3-,
=t+2(1)求
•; (2)试用t来表示
•的值;(3)若
与
的夹角为钝角,试求实数t的取值范围.
查看答案和解析>>
(1)已知
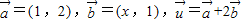
,
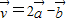
,且
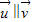
,求实数x;
(2)已知向量
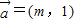
,
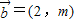
的夹角为钝角,求m的取值范围.
查看答案和解析>>
(1)已知
=(1,2),=(x,1),=+2,
=2-,且
∥,求实数x;
(2)已知向量
=(m,1),
=(2,m)的夹角为钝角,求m的取值范围.
查看答案和解析>>
(1)已知
=(1,2),=(x,1),=+2,
=2-,且
∥,求实数x;
(2)已知向量
=(m,1),
=(2,m)的夹角为钝角,求m的取值范围.
查看答案和解析>>

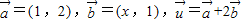 ,
,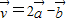 ,且
,且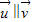 ,求实数x;
,求实数x;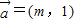 ,
,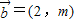 的夹角为钝角,求m的取值范围.
的夹角为钝角,求m的取值范围.