在数列{an},{bn}中.a1=2, b1=4.且成等差数列.成等比数列() (Ⅰ)求a2, a3, a4及b2, b3, b4.由此猜测{an},{bn}的通项公式.并用数学归纳法证明你的结论, (Ⅱ)证明: 【
查看更多】
题目列表(包括答案和解析)
在数列{a
n},{b
n}中,a
1=2,b
1=4,且a
n,b
n,a
n+1成等差数列,b
n,a
n+1,b
n+1成等比数列.
(1)求a
2,a
3,a
4及b
2,b
3,b
4,由此猜测{a
n},{b
n}的通项公式,并证明你的结论;
(2)证明:
++…+<.
查看答案和解析>>
在数列{a
n},{b
n}中,a
1=2,b
1=4,且a
n,b
n,a
n+1成等差数列,b
n,a
n+1,b
n+1成等比数列(n∈N
*).
(Ⅰ)求a
2,a
3,a
4和b
2,b
3,b
4,由此猜测{a
n},{b
n}的通项公式;
(Ⅱ)证明你的结论;
(Ⅲ)证明:
+
+…+
<
.
查看答案和解析>>
在数列{a
n},{b
n}中,a
1=2,b
1=4,且a
n,b
n,a
n+1成等差数列,b
n,a
n+1,b
n+1成等比数列(n∈N
*)
(Ⅰ)求a
2,a
3,a
4及b
2,b
3,b
4;
(Ⅱ)求{a
n},{b
n}的通项公式;
(Ⅲ)证明:
++…+<.
查看答案和解析>>
在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列.
(1)求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
(2)证明: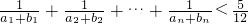 .
.
查看答案和解析>>
在数列{a
n},{b
n}中,a
1=2,b
1=4,且a
n,b
n,a
n+1成等差数列,b
n,a
n+1,b
n+1成等比数列,
(1)求a
2,a
3,a
4及b
2,b
3,b
4,由此猜测{a
n},{b
n}的通项公式,并证明你的结论;
(2)证明:

。
查看答案和解析>>

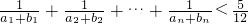 .
. 。
。