
题目列表(包括答案和解析)
(05北京卷)已知函数f(x)=-x3+3x2+9x+a,
(I)求f(x)的单调递减区间;
(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
(A卷)设f(x)是定义域为R,最小正周期为![]() 的函数,若f(x)=
的函数,若f(x)= 则
则![]() 等于
等于
A.1
B.![]()
C.0
D.![]()
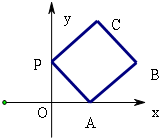 (北京卷理14)如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为
(北京卷理14)如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为(04年北京卷文)(14分)
函数f(x)定义在[0,1]上,满足![]() 且f(1)=1,在每个区间
且f(1)=1,在每个区间![]() =1,2,…)上, y=f(x) 的图象都是平行于x轴的直线的一部分.
=1,2,…)上, y=f(x) 的图象都是平行于x轴的直线的一部分.
(Ⅰ)求f(0)及![]() 的值,并归纳出
的值,并归纳出![]() )的表达式;
)的表达式;
(Ⅱ)设直线![]() 轴及y=f(x)的图象围成的矩形的面积为
轴及y=f(x)的图象围成的矩形的面积为![]() , 求a1,a2及
, 求a1,a2及![]() 的值.
的值.
(05年北京卷理)(14分)
设![]() 是定义在[0,1]上的函数,若存在
是定义在[0,1]上的函数,若存在![]() ,使得
,使得![]() 在[0,
在[0,![]() ]上单调递增,在[
]上单调递增,在[![]() ,1]单调递减,则称
,1]单调递减,则称![]() 为[0,1]上的单峰函数,
为[0,1]上的单峰函数,![]() 为峰点,包含峰点的区间为含峰区间
为峰点,包含峰点的区间为含峰区间![]() 对任意的[0,1]上的单峰函数
对任意的[0,1]上的单峰函数![]() ,下面研究缩短其含峰区间长度的方法
,下面研究缩短其含峰区间长度的方法![]()
(Ⅰ)证明:对任意的![]()
![]() ,
, ![]() ,若
,若![]() ,则(0,
,则(0,![]() )为含峰区间;若
)为含峰区间;若![]() ,则(
,则(![]() ,1)为含峰区间;
,1)为含峰区间;
(Ⅱ)对给定的![]() (0<
(0<![]() <0.5),证明:存在
<0.5),证明:存在![]()
![]() ,满足
,满足![]() ,使得由(Ⅰ)确定的含峰区间的长度不大于0.5+
,使得由(Ⅰ)确定的含峰区间的长度不大于0.5+![]() ;
;
(Ⅲ)选取![]()
![]() ,
,![]() 由(Ⅰ)可确定含峰区间为(0,
由(Ⅰ)可确定含峰区间为(0,![]() )或(
)或(![]() ,1),在所得的含峰区间内选取
,1),在所得的含峰区间内选取![]() ,由
,由![]() 与
与![]() 或
或![]() 与
与![]() 类似地可确定是一个新的含峰区间.在第一次确定的含峰区间为(0,
类似地可确定是一个新的含峰区间.在第一次确定的含峰区间为(0,![]() )的情况下,试确定
)的情况下,试确定![]() 的值,满足两两之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34
的值,满足两两之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34![]()
(区间长度等于区间的右端点与左端点之差)![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com