
题目列表(包括答案和解析)
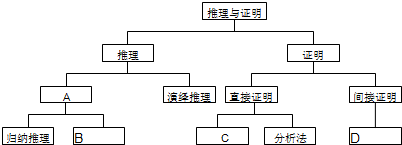
 4、如图是人教A版教材选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“三段论”,则应该放在图中( )
4、如图是人教A版教材选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“三段论”,则应该放在图中( )| f(x) | g(x) |
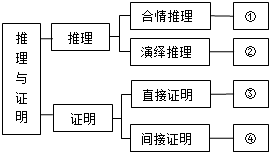
下图是选修1-2中《推理与证明》一章的知识结构图, 请把
“①合情推理”,“② 类比推理”,“③综合法”,“④反证法”填入适当的方框内.(填序号即可)
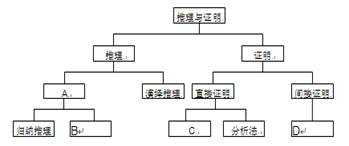
A填___ _B填_____ _C填_____ _D填________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com