
题目列表(包括答案和解析)
已知函数 ,(
,(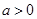 ),
),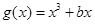
(1)若曲线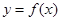 与曲线
与曲线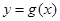 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值
(2)当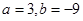 时,若函数
时,若函数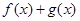 在区间[k,2]上的最大值为28,求k的取值范围
在区间[k,2]上的最大值为28,求k的取值范围
【解析】(1)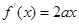 ,
,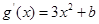
∵曲线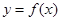 与曲线
与曲线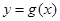 在它们的交点(1,c)处具有公共切线
在它们的交点(1,c)处具有公共切线
∴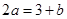 ,
,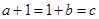
∴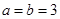
(2)当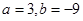 时,
时,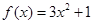 ,
,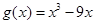 ,
,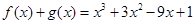
令 ,则
,则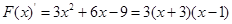 ,令
,令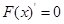 ,
, ∴
∴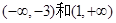 为单调递增区间,
为单调递增区间,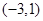 为单调递减区间,其中F(-3)=28为极大值,所以如果区间[k,2]最大值为28,即区间包含极大值点
为单调递减区间,其中F(-3)=28为极大值,所以如果区间[k,2]最大值为28,即区间包含极大值点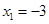 ,所以
,所以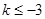
【考点定位】此题应该说是导数题目中较为常规的类型题目,考查的切线,单调性,极值以及最值问题都是课本中要求的重点内容,也是学生掌握比较好的知识点,在题目中能够发现F(-3)=28,和分析出区间[k,2]包含极大值点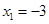 ,比较重要
,比较重要
“……一千英磅赠给波士顿的居民,如果他们接受了这一千英磅,那么这笔钱应该托付给一些挑选出来的公民,他们得把这些钱按每年5%的利率借给一些年轻的手工业者去生息.这些钱过了100年增加到131 000英磅.我希望那时候用100 000英磅来建立一所公共建筑物,剩下的31 000英磅拿去继续生息100年……”
请你计算一下富兰克林的遗嘱能实现吗?
富兰克林(Benjamin Franklin,1706~1790)是美国著名的科学家、社会活动家,他的业绩遍及十九个科技领域.“你热爱生命吗?那么别浪费时间,因为时间是组成生命的材料.”就是这位科学家留下的名言.这位科学家死后只留下了一千英磅的遗产,然而他却留下了几十万英磅的遗嘱,这份有趣的遗嘱内容是这样的:
“……一千英磅赠给波士顿的居民,如果他们接受了这一千英磅,那么这笔钱应该托付给一些挑选出来的公民,他们得把这些钱按每年5%的利率借给一些年轻的手工业者去生息.这些钱过了100年增加到131 000英磅.我希望那时候用100 000英磅来建立一所公共建筑物,剩下的31 000英磅拿去继续生息100年……”
请你计算一下富兰克林的遗嘱能实现吗?
(本小题满分14分)
某校学生社团心理学研究小组在对学生在一节课中上课注意力集中情况的调查研究中,发现其注意力指数 与听课时间
与听课时间 之间的关系满足如图所示的曲线.当
之间的关系满足如图所示的曲线.当 时,曲线是二次函数图象的一部分,
时,曲线是二次函数图象的一部分, 为其对称轴;当
为其对称轴;当 时,曲线是函数
时,曲线是函数 (
( 且
且 )图象的一部分.根据专家研究,当注意力指数
)图象的一部分.根据专家研究,当注意力指数 大于80时听课效果最佳.
大于80时听课效果最佳.
(1) 试求 的函数关系式;
的函数关系式;
(2) 老师在什么时段内安排重点内容能使得学生听课效果最佳?
请说明理由.

A.|x+a| B.{0}∈N
C.集合与简易逻辑 D.真子集
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com