
题目列表(包括答案和解析)
 (2007?深圳二模)如图甲所示,质量为m=50g,长l=10cm的铜棒,用长度亦为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度B=1/3T.未通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流的大小.
(2007?深圳二模)如图甲所示,质量为m=50g,长l=10cm的铜棒,用长度亦为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度B=1/3T.未通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流的大小.| F |
| mg |
| BIl |
| mg |
| mgtanθ |
| Bl |
0.05×10×
| ||
|
| mg(1-cos°) |
| BIsin37° |
| 0.05×10×(1-0.8) | ||
|
| F |
| mg |
| BIl |
| mg |
| mgtan370 |
| Bl |
0.05×10×
| ||
| 0.5×0.1 |
| mgl(1-cos370) |
| Blsin2370 |
| 0.05×10×(1-0.8) |
| 0.5×0.1×(0.6)2 |
| 50 |
| 9 |

如图所示,质量为0.05kg,长l=0.1m的铜棒,用长度也为l的两根轻软导线水平悬挂在竖直向上的匀强磁场中,磁感应强度为B=0.5T.不通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流多大?(不考虑棒摆动过程中产生的感应电流,g取10N/kg)
同学甲的解法如下:对铜棒受力分析如图所示:
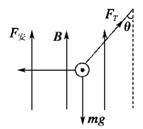
当最大偏转角θ=37°时,棒受力平衡,有:
FTcosθ=mg,FTsinθ=F安=BIl
得I==A=7.5A
同学乙的解法如下:
F安做功:WF=Fx1=BIlsin37°×lsin37°=BI(lsin37°)2
重力做功:
WG=-mgx2=-mgl(1-cos37°)
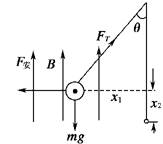
由动能定理得:WF+WG=0
代入数据解得:I=A≈5.56A
请你对甲、乙两同学的解法作出评价:若你对两者都不支持,则给出你认为正确的解答.
如图所示,质量为0.05kg,长l=0.1m的铜棒,用长度也为l的两根轻软导线水平悬挂在竖直向上的匀强磁场中,磁感应强度为B=0.5T.不通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流多大?(不考虑棒摆动过程中产生的感应电流,g取10N/kg)
同学甲的解法如下:对铜棒受力分析如图所示:
当最大偏转角θ=37°时,棒受力平衡,有:
FTcosθ=mg,FTsinθ=F安=BIl
得I==A=7.5A
同学乙的解法如下:
F安做功:WF=Fx1=BIlsin37°×lsin37°=BI(lsin37°)2
重力做功:
WG=-mgx2=-mgl(1-cos37°)
由动能定理得:WF+WG=0
代入数据解得:I=A≈5.56A
请你对甲、乙两同学的解法作出评价:若你对两者都不支持,则给出你认为正确的解答.
(15分)如图甲所示,质量为m,长为l的铜棒,用长度亦为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度为B,未通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度![]() ,求此棒中恒定电流的大小。
,求此棒中恒定电流的大小。

同学甲的解法如下:对铜棒进行受力分析,通电时导线向外偏转,说明安培力方向垂直电流和磁场方向向外,受力如图乙所示(侧视图)。当最大偏转角θ时,棒受力平衡,有: ![]() , 得
, 得![]()
同学乙的解法如下:铜棒向外偏转过程中,导线拉力不做功,如图丙所示。
F做功为:![]()
重力做功为:![]()
由动能定理得:![]() ,
,
得![]()
请你对同学甲和乙的解答作出简要的评价;若你对两者都不支持,则给出你认为正确的解答。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com