
题目列表(包括答案和解析)
| |||||||||||
| x2 |
| 4 |
| 2 |
| OA |
| OB |
⊙O1和⊙O2的极坐标方程分别为 ,
, .
.
⑴把⊙O1和⊙O2的极坐标方程化为直角坐标方程;
⑵求经过⊙O1,⊙O2交点的直线的直角坐标方程.
【解析】本试题主要是考查了极坐标的返程和直角坐标方程的转化和简单的圆冤啊位置关系的运用
(1)中,借助于公式 ,
, ,将极坐标方程化为普通方程即可。
,将极坐标方程化为普通方程即可。
(2)中,根据上一问中的圆的方程,然后作差得到交线所在的直线的普通方程。
解:以极点为原点,极轴为x轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(I) ,
, ,由
,由 得
得 .所以
.所以 .
.
即 为⊙O1的直角坐标方程.
为⊙O1的直角坐标方程.
同理 为⊙O2的直角坐标方程.
为⊙O2的直角坐标方程.
(II)解法一:由 解得
解得 ,
,
即⊙O1,⊙O2交于点(0,0)和(2,-2).过交点的直线的直角坐标方程为y=-x.
解法二: 由 ,两式相减得-4x-4y=0,即过交点的直线的直角坐标方程为y=-x
,两式相减得-4x-4y=0,即过交点的直线的直角坐标方程为y=-x
这个算法又叫“韩信点兵”.相传韩信才略过人,领兵打仗时,为了对敌方保密,从不点自己军队的人数,只是让他的士兵以三人一排很快地从他面前过去,再以五人一排走一次,最后以七人一排走过去,由于队伍走得很快,别人根本来不及数有多少人.然而韩信只对各队士兵的最后一排掠一眼,就知道总数了,他利用的就是上面的这个口诀.
画出程序框图,并编写程序解决“韩信点兵”问题.
古希腊数学家丢番图(公元250年前后)在《算术》中就提到了一元二次![]() 方程的问题,不过当时古希腊人还没有寻求到它的求根公式,只能用图解等方法来求解。在欧几里得的《几何原本》中,形如
方程的问题,不过当时古希腊人还没有寻求到它的求根公式,只能用图解等方法来求解。在欧几里得的《几何原本》中,形如![]() (a>0,b>0)的方程的图解法是:如图,以
(a>0,b>0)的方程的图解法是:如图,以![]() 和b为两直角边做Rt△ABC,再在斜边上截取
和b为两直角边做Rt△ABC,再在斜边上截取![]() ,则AD的长就是所求方程的解。
,则AD的长就是所求方程的解。
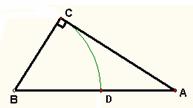
(1)请用含字母a、b的代数式表示AD的长。
(2)请利用你已学的知识说明该图解法的正确性,并说说这种解法的遗憾之处。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com