
题目列表(包括答案和解析)
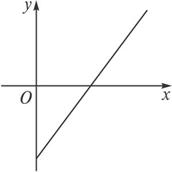

对于上面给出的四个图象,以下说法正确的是
A.①反映了建议(2),③反映了建议(1) B.①反映了建议(1),③反映了建议(2)
C.②反映了建议(1),③反映了建议(2) D.④反映了建议(1),④反映了建议(1)
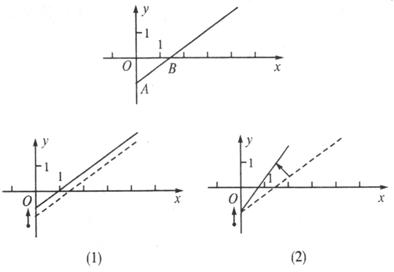
请你根据图象用简练的语言叙述:
建议(1)是_____________________________________________;
建议(2)是_____________________________________________.
下列可以看成算法的是( )
A.学习数学时,课前预习,课上认真听讲并记好笔记,课下先复习再做作业,之后做适当的练习题
B.今天餐厅的饭真好吃
C.这道数学题难做
D.方程2x2-x+1=0无实数根
|
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com