
题目列表(包括答案和解析)
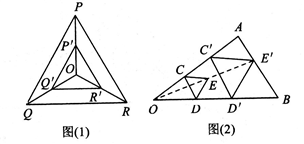
 、点P
、点P 、点O
、点O

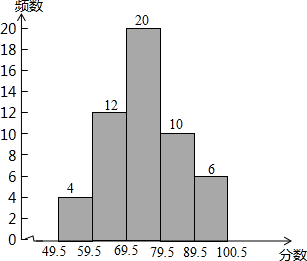 某学校为推动信息技术的发展,举行了电脑设计作品比赛,各个班随机派学生代表参加,现将比赛成绩进行整理后分成五组,并绘制成如图所示的频数分布直方图.请根据统计图提供的信息,解答下列问题:
某学校为推动信息技术的发展,举行了电脑设计作品比赛,各个班随机派学生代表参加,现将比赛成绩进行整理后分成五组,并绘制成如图所示的频数分布直方图.请根据统计图提供的信息,解答下列问题: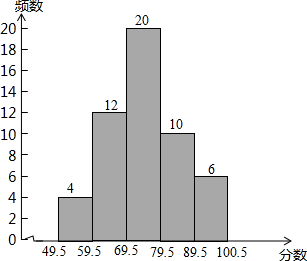 某学校为推动信息技术的发展,举行了电脑设计作品比赛,各个班随机派学生代表参加,现将比赛成绩进行整理后分成五组,并绘制成如图所示的频数分布直方图.请根据统计图提供的信息,解答下列问题:
某学校为推动信息技术的发展,举行了电脑设计作品比赛,各个班随机派学生代表参加,现将比赛成绩进行整理后分成五组,并绘制成如图所示的频数分布直方图.请根据统计图提供的信息,解答下列问题:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com