
题目列表(包括答案和解析)

![]() 内的概率为
内的概率为![]() .
.
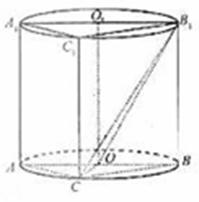
(i)当点C在圆周上运动时,求![]() 的最大值;
的最大值;
(ii)记平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
![]() ,当
,当![]() 取最大值时,
取最大值时,
求![]() 的值。
的值。
正态总体的概率密度函数![]() (xÎR),则正态总体在区间(1,4)内取值的概率为________。
(xÎR),则正态总体在区间(1,4)内取值的概率为________。
在区间 内任取两个数
内任取两个数 ,则“
,则“ ”的概率是 。
”的概率是 。
 内任取两个数
内任取两个数 ,则“
,则“ ”的概率是 。
”的概率是 。
一、选择题:本大题共10小题,每小题5分,共50分。
1.B 2.D 3.A 4.A 5.B 6.C 7.C 8.C 9.A 10.B
二、填空题:本大题共5小题,每小题4分,共20分。
11.5 12. 13.
13. 14.7 15.
14.7 15.
三、解答题:本大题共6小题,共80分。
16.解:(I)由三角函数的定义可知

又 为正三角形,
为正三角形,


(Ⅱ)
圆的面积为 。
。
 该点落在
该点落在 内的概率
内的概率
17.解:(I)依题意,每个月更新的车辆数构成一个首项为 ,公差为
,公差为 的等差数列,设第
的等差数列,设第
 个月更新的车辆数为
个月更新的车辆数为 ,则
,则
 该市的出租车总数
该市的出租车总数 (辆)
(辆)
(Ⅱ)依题意,每个月更新的车辆数构成一个首项为 ,公比为1.1的等比数列,则第
,公比为1.1的等比数列,则第
个月更新的车辆数 ,设至少需要
,设至少需要 个月才能更新完毕,
个月才能更新完毕,

 个月更新的车辆总数
个月更新的车辆总数 ,
,
即 ,由参数数据可得
,由参数数据可得
故以此速度进行更新,至少需要37个月才能更新完该市所有的出租车
18.解(I) ,
, 为等腰直角三角形,
为等腰直角三角形,

(Ⅱ)如图建立空间直角坐标系,则

 设平面
设平面 的一个法向量为
的一个法向量为 ,
,
则有 得
得
 平面
平面 的一个法向量
的一个法向量
而 的一个法向量
的一个法向量

 平面
平面 与平面
与平面 所成的角的余弦值
所成的角的余弦值
(Ⅲ) ,
,

设平面 的法向量为
的法向量为 ,则有
,则有
 平面
平面 的一个法向量为
的一个法向量为
若要使得 面
面 ,则要
,则要 ,即
,即
解得 ,
,  当
当 时,
时,  面
面
19.解法一:
(I)设椭圆方程为 ,由题意知
,由题意知

故椭圆方程为
(Ⅱ)由(I)得 ,所以
,所以 ,设
,设 的方程为
的方程为 (
( )
)
代入 ,得
,得
设 则
则



由 ,
,
 当
当 时,有
时,有 成立。
成立。
(Ⅲ)在 轴上存在定点
轴上存在定点 ,使得
,使得 、
、 、
、 三点共线。
三点共线。
依题意知 ,直线BC的方程为
,直线BC的方程为 ,
,
令 ,则
,则

 的方程为
的方程为 、
、 在直线
在直线 上,
上,


 在
在 轴上存在定点
轴上存在定点 ,使得
,使得 、
、 、
、 三点共线。
三点共线。
解法二:(I)同解法一。
(Ⅱ)由(I)得 ,所以
,所以 。
。
设 的方程为
的方程为
代入 ,得
,得
设 则
则




 当
当 时,有
时,有 成立。
成立。
(Ⅲ)在 轴上存在定点
轴上存在定点 ,使得
,使得 、
、 、
、 三点共线。
三点共线。
设存在 使得
使得 、
、 、
、 三点共线,则
三点共线,则 ,
,
 ,
,

即

 ,
, 。
。
所以,存在 ,使得
,使得 、
、 、
、 三点共线。
三点共线。
20.解:(I)
当 时,
时,
由 或
或 。
。
x
(0,1)
1


+
―

单调递增
极大值
单调递减
 时,
时, ,无极小值。
,无极小值。
(Ⅱ) 存在单调递减区间,
存在单调递减区间,
 在
在 内有解,即
内有解,即 在
在 内有解。
内有解。
若 ,则
,则 ,
, 在
在 单调递增,不存在单调递减区间;
单调递增,不存在单调递减区间;
若 ,则函数
,则函数 的图象是开口向上的抛物线,且恒过点(0,1),要
的图象是开口向上的抛物线,且恒过点(0,1),要
使 在
在 内有解,则应有
内有解,则应有
 或
或 ,由于
,由于 ,
, ;
;
若 ,则函数
,则函数 的图象是开口向下的抛物线,且恒过点(0,1),
的图象是开口向下的抛物线,且恒过点(0,1),
 在
在 内一定有解。
内一定有解。
综上, 或
或 。
。
(Ⅲ)依题意: ,假设结论不成立,
,假设结论不成立,
则有
①―②,得

由③得,
 即
即
设 ,则
,则 ,
,
令
 ,
, 在(0,1)上为增函数。
在(0,1)上为增函数。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com