
题目列表(包括答案和解析)
(2005
上海,21)对定义域分别是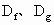 的函数y=f(x)、y=g(x),规定:函数
的函数y=f(x)、y=g(x),规定:函数
(1)
若函数 ,
, ,写出函数h(x)的解析式;
,写出函数h(x)的解析式;
(2)
求问题(1)中函数h(x)的值域;(3)
若g(x)=f(x+α),其中α是常数,且α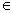 [0,π],请设计一个定义域为R的函数y=f(x),及一个α的值,使得h(x)=cos 4x,并予以证明.
[0,π],请设计一个定义域为R的函数y=f(x),及一个α的值,使得h(x)=cos 4x,并予以证明.| 16 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
| 第1列 | 第2列 | 第3列 | … | 第n列 | |
| 第1行 | 1 | 1 | 1 | … | 1 |
| 第2行 | q | ||||
| 第3行 | q2 | ||||
| … | … | ||||
| 第n行 | qn-1 |
| 3 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
(本小题满分12分)
某单位选派甲、乙、丙三人组队参加“2010上海世博会知识竞赛”,甲、乙、丙三人在同时回答一道问题时,已知甲答对的概率是 ,甲、丙两人都答错的概率是
,甲、丙两人都答错的概率是 ,乙、丙两人都答对的概率是
,乙、丙两人都答对的概率是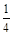 ,规定每队只要有一人答对此题则记该队答对此题.
,规定每队只要有一人答对此题则记该队答对此题.
(Ⅰ)求该单位代表队答对此题的概率;
(Ⅱ)此次竞赛规定每队都要回答10道必答题,每道题答对得20分,答错除该题不得分外还要倒扣去10分.若该单位代表队答对每道题的概率相等且回答任一道题的对错对回答其它题没有影响,求该单位代表队必答题得分的期望(精确到1分).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com