
题目列表(包括答案和解析)
某高中社团进行社会实践,对
[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”.通过调查分别得到如下图所示统计表和如图所示各年龄段人数频率分布直方图:
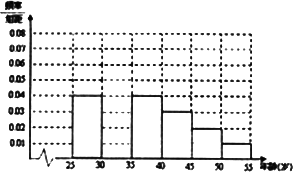
请完成下列问题:
(1)补全频率分布直方图,并求n,a,p的值;
(2)从[40,45)和[45,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,求选取的3名领队年龄在[40,45)岁的人数为X,求X的分布列和期望E(X).
为了考查某校的教学水平,将抽查这个学校高三年级的部分学生的本学年考试成绩进行考察,为了全面地反映实际情况,采取以下三种方式进行抽查:(已知该校高三年级共有20个教学班,并且每个班内的学生已经按随机方式编好了学号,假定该校每班学生人数都相同)
(1)从全年级20个班中任意抽取一个班,再从该班中任意抽取20人,考查他们的学习成绩;
(2)每个班都抽取1人,共计20人,考查这20个学生的成绩;
(3)把学生按成绩分成优秀、良好、普通三个级别,从其中共抽取100名学生进行考查.(已知若按成绩分,该校高三学生中优秀共150人,良好生共600人,普通生共250人)
根据上面的叙述,试回答下列问题:
①上面三种抽取方式中,其总体、个体、样本分别指什么?每一种抽取方式抽取的样本中,其样本容量分别是多少?
②上面三种抽取方式中各自采用何种抽取样本的方法?
| 病症及代号 | 普通病症A1 | 复诊病症A2 | 常见病症A3 | 疑难病症A4 | 特殊病症A5 |
| 人数 | 100 | 300 | 200 | 300 | 100 |
| 每人就诊时间 (单位:分钟) |
3 | 4 | 5 | 6 | 7 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com