
题目列表(包括答案和解析)
把函数 的图象按向量
的图象按向量 平移得到函数
平移得到函数 的图象.
的图象.
(1)求函数 的解析式; (2)若
的解析式; (2)若 ,证明:
,证明: .
.
【解析】本试题主要考查了函数 平抑变换和运用函数思想证明不等式。第一问中,利用设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 ,便可以得到结论。第二问中,令
,便可以得到结论。第二问中,令 ,然后求导,利用最小值大于零得到。
,然后求导,利用最小值大于零得到。
(1)解:设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 得y-2=ln(x+1)-2即y=ln(x+1),所以
得y-2=ln(x+1)-2即y=ln(x+1),所以 .……4分
.……4分
(2) 证明:令 ,……6分
,……6分
则 ……8分
……8分
 ,∴
,∴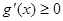 ,∴
,∴ 在
在 上单调递增.……10分
上单调递增.……10分
故 ,即
,即
心脏跳动时,血压在增加或减少,血压的最大值、最小分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数80 mmHg~120 mmHg称为标准值.
设某人在某一时刻的血压满足函数式p(t)=125+25sin(170πt),其中p(t)为血压(mmHg),t为时间(min),试解答下列问题:
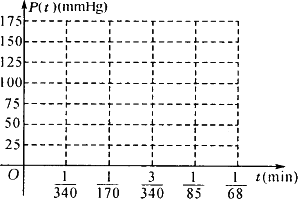
(1)求函数p(t)的周期;
(2)求此人每分钟心跳的次数;
(3)用“五点法”在给定的坐标系中作出p(t)在一个周期上的简图;
(4)写出此人的血压在血压计上的读数.
我们用min{S1,S2,…,Sn}和max{S1,S2,…,Sn}分别表示实数S1,S2,…,Sn中的最小者和最大者.
(1)设f(x)=min{sinx,cosx},g(x)=max{sinx,cosx},x∈[0,2π],函数f(x)的值域为A,函数g(x)的值域为B,求A∩B;
(2)数学课上老师提出了下面的问题:设a1,a2,an为实数,x∈R,求函数![]() (x1<x2<xn∈R=的最小值或最大值.为了方便探究,遵循从特殊到一般的原则,老师让学生先解决两个特例:求函数
(x1<x2<xn∈R=的最小值或最大值.为了方便探究,遵循从特殊到一般的原则,老师让学生先解决两个特例:求函数![]() 和
和![]() 的最值.学生甲得出的结论是:[f(x)]min=min{f(-2),f(-1),f(1)},且f(x)无最大值.学生乙得出的结论是:[g(x)]max=max{g(-1),g(1),g(2)},且g(x)无最小值.请选择两个学生得出的结论中的一个,说明其成立的理由;
的最值.学生甲得出的结论是:[f(x)]min=min{f(-2),f(-1),f(1)},且f(x)无最大值.学生乙得出的结论是:[g(x)]max=max{g(-1),g(1),g(2)},且g(x)无最小值.请选择两个学生得出的结论中的一个,说明其成立的理由;
(3)试对老师提出的问题进行研究,写出你所得到的结论并加以证明(如果结论是分类的,请选择一种情况加以证明).
| |||||||||||||||
已知函数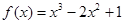 .
.
(1)求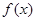 在区间
在区间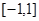 上的最大值;
上的最大值;
(2)若函数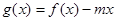 在区间
在区间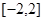 上存在递减区间,求实数m的取值范围.
上存在递减区间,求实数m的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用,求解函数的最值。第一问中,利用导数求解函数的最值,首先求解导数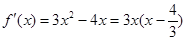 ,然后利用极值和端点值比较大小,得到结论。第二问中,我们利用函数在
,然后利用极值和端点值比较大小,得到结论。第二问中,我们利用函数在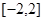 上存在递减区间,即
上存在递减区间,即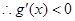 在
在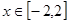 上有解,即
上有解,即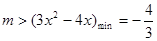 ,即可,可得到。
,即可,可得到。
解:(1)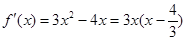 ,
,
令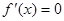 ,解得
,解得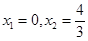 ……………3分
……………3分
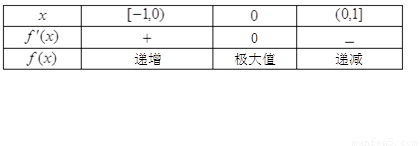
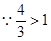 ,
,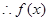 在
在 上为增函数,在
上为增函数,在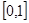 上为减函数,
上为减函数,
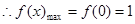 .
…………6分
.
…………6分
(2)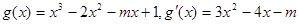
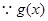 在
在 上存在递减区间,
上存在递减区间,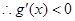 在
在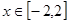 上有解,……9分
上有解,……9分
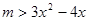 在
在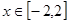 上有解,
上有解,
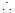
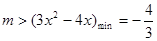 ,
,
所以,实数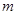 的取值范围为
的取值范围为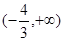
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com