练习册

  • 练习册
  • 试题
    问题1．( 北京)矩形的两条对角线相交于点.边所在直线的方程为.点在边所在直线上． 求边所在直线的方程,求矩形外接圆的方程,若动圆过点.且与矩形的外接圆外切.求动圆的圆心的轨迹方程． 问题2．(福建)如图.已知点. 直线:.为平面上的动点.过作直线 的垂线.垂足为点.且． (Ⅰ)求动点的轨迹的方程, (Ⅱ)过点的直线交轨迹于两点.交直线 于点.已知..求的值, 问题3．倾斜角为的直线交椭圆于两点.求线段中点的轨迹方程 问题4．双曲线关于直线对称的曲线方程是 已知抛物线..问是否存在过点的直线.使抛物线上存在不同的两点关于直线对称?如果存在.求出直线斜率的取值范围,如果不存在.请说明理由. 【查看更多】

     

    题目列表(包括答案和解析)

    阅读理解
    （1）教材27页有如下内容：
    分别观察三个图象，你看出哪些变化规律

    （2）教材是这样定义偶函数的（如图文字）

    问题1：辅导班的小王认为 f（x）=x2，x∈[-5，5）是偶函数，理由如下：对于函数定义域内的任意一个x，f（-x）=（-x）2=x2=f（x），所以该函数式偶函数，你认为对吗？为什么？
    问题2：奇函数的定义是？

    查看答案和解析>>

    问题1：已知函数f(x)=
    x
    1+x
    ，则f(
    1
    10
    )+f(
    1
    9
    )+    …+f(
    1
    2
    )+f(1)+f(2)+    …+f（9）+f（10）=
    19
    2
    19
    2
    ．
    我们若把每一个函数值计算出，再求和，对函数值个数较少时是常用方法，但函数值个数较多时，运算就较繁锁．观察和式，我们发现f(
    1
    2
    )+f(2)    、…、f(
    1
    9
    )+f(9)    、f(
    1
    10
    )+f(10)    可一般表示为f(
    1
    x
    )+f(x)    =
    1
    x
    1+
    1
    x
    +
    x
    1+x
    =
    1
    1+x
    +
    x
    1+x
    =
    1+x
    1+x
    =1    为定值，有此规律从而很方便求和，请求出上述结果，并用此方法求解下面问题：
    问题2：已知函数f(x)=
    1
    2x+
    		2
    ，求f（-2007）+f（-2006）+…+f（-1）+f（0）+f（1）+…+f（2007）+f（2008）的值．

    查看答案和解析>>

    17、如图，是求[1，1000]内所有奇数的和的一个程序框图，
    问题1：把程序框图补充完整．
    （1）处填
    s=s+i
    ；
    （2）处填
    i=i+2
    ；
    问题2：根据程序框图写出相应的程序．

    查看答案和解析>>

    问题1：求三维空间至多被n个平面分割的区域数F（n）．
    问题2：求一个平面至多被n条直线分割的区域数G（n）．
    问题3：求一直线至多被n个点分成的段数S（n）．

    查看答案和解析>>

    .甲、乙两同学利用暑假到某县进行社会实践,对该县的养鸡场连续六年来的规模进行调查研究,得到如下两个不同的信息图.(A)图表明:从第1年平均每个养鸡场出产1万只鸡上升到第6年平均每个养鸡场出产2万只鸡;(B)图表明:由第1年养鸡场个数30个减少到第6年的10个.

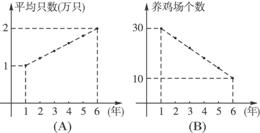
    请你根据提供的信息解答下列问题:

    (1)第二年的养鸡场的个数及全县出产鸡的总只数各是多少?

    (2)哪一年的规模最大?为什么?

    查看答案和解析>>


    同步练习册答案