
题目列表(包括答案和解析)
已知曲线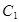 上任意一点
上任意一点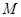 到直线
到直线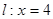 的距离是它到点
的距离是它到点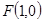 距离的
距离的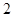 倍;曲线
倍;曲线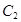 是以原点为顶点,
是以原点为顶点,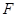 为焦点的抛物线.
为焦点的抛物线.
(Ⅰ)求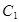 ,
,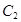 的方程;
的方程;
(Ⅱ)过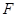 作两条互相垂直的直线
作两条互相垂直的直线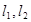 ,其中
,其中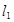 与
与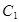 相交于点
相交于点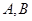 ,
,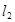 与
与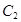 相交于点
相交于点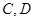 ,求四边形
,求四边形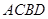 面积的取值范围.
面积的取值范围.
(1)P点坐标;
(2)|AB|的值.
已知点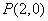 与
与 ,且点M到点P的距离是它到点Q的距离的
,且点M到点P的距离是它到点Q的距离的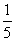 ,求点M的轨迹方程。
,求点M的轨迹方程。
已知点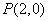 与
与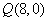 ,且点M到点P的距离是它到点Q的距离的
,且点M到点P的距离是它到点Q的距离的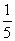 ,求点M的轨迹方程。
,求点M的轨迹方程。
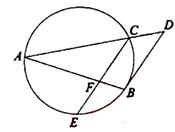
如图,已知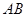 和
和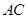 是圆的两条弦,过点
是圆的两条弦,过点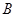 作圆的切线与
作圆的切线与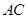 的延长线相交于
的延长线相交于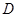 .过点
.过点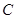 作
作 的平行线与圆交于点
的平行线与圆交于点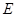 ,与
,与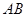 相交于点
相交于点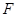 ,
,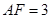 ,
,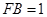 ,
,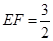 ,则线段
,则线段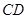 的长为 .
的长为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com