
题目列表(包括答案和解析)
如图,△ABC与△BCD是一副三角板,它们所在的两个平面互相垂直.若AB=AC,∠BAC=∠BCD=90°,∠CBD=30°.
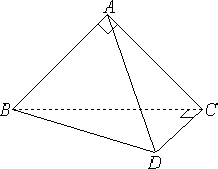
(Ⅰ)求证:三棱锥A-BCD的四个面都是直角三角形;
(Ⅱ)求二面角A-BD-C的正切值.
 已知一几何体的三视图如图,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择5个顶点,它们可能是如下各种几何形体的5个顶点,这些几何形体是(写出所有正确结论的编号)
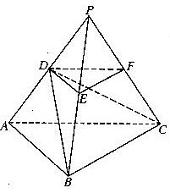
已知一几何体的三视图如图,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择5个顶点,它们可能是如下各种几何形体的5个顶点,这些几何形体是(写出所有正确结论的编号)如图,P—ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点, 截面DEF∥底面ABC, 且棱台DEF—ABC与棱锥P—ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
(1)证明:P—ABC为正四面体;
(2)若PD=![]() PA, 求二面角D—BC—A的大小;(结果用反三角函数值表示)
PA, 求二面角D—BC—A的大小;(结果用反三角函数值表示)
(3)设棱台DEF—ABC的体积为V, 是否存在体积为V且各棱长均相等的直平行六面体,使得它与棱台DEF—ABC有相同的棱长和? 若存在,请具体构造出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.
(1)证明:P—ABC为正四面体;
(2)若PD=![]() PA, 求二面角D—BC—A的大小;(结果用反三角函数值表示)
PA, 求二面角D—BC—A的大小;(结果用反三角函数值表示)
(3)设棱台DEF—ABC的体积为V, 是否存在体积为V且各棱长均相等的直平行六面体,使得它与棱台DEF—ABC有相同的棱长和? 若存在,请具体构造出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.

 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)| 1 | 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com