
题目列表(包括答案和解析)
已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当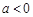 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
⊙O1和⊙O2的极坐标方程分别为 ,
, .
.
⑴把⊙O1和⊙O2的极坐标方程化为直角坐标方程;
⑵求经过⊙O1,⊙O2交点的直线的直角坐标方程.
【解析】本试题主要是考查了极坐标的返程和直角坐标方程的转化和简单的圆冤啊位置关系的运用
(1)中,借助于公式 ,
, ,将极坐标方程化为普通方程即可。
,将极坐标方程化为普通方程即可。
(2)中,根据上一问中的圆的方程,然后作差得到交线所在的直线的普通方程。
解:以极点为原点,极轴为x轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(I) ,
, ,由
,由 得
得 .所以
.所以 .
.
即 为⊙O1的直角坐标方程.
为⊙O1的直角坐标方程.
同理 为⊙O2的直角坐标方程.
为⊙O2的直角坐标方程.
(II)解法一:由 解得
解得 ,
,
即⊙O1,⊙O2交于点(0,0)和(2,-2).过交点的直线的直角坐标方程为y=-x.
解法二: 由 ,两式相减得-4x-4y=0,即过交点的直线的直角坐标方程为y=-x
,两式相减得-4x-4y=0,即过交点的直线的直角坐标方程为y=-x
(本小题满分12分)
阅读下面内容,思考后做两道小题。
在一节数学课上,老师给出一道题,让同学们先解,题目是这样的:
已知函数f(x)=kx+b,1≤f(1)≤3,-1≤f(-1)≤1,求Z=f(2)的取值范围。
题目给出后,同学们马上投入紧张的解答中,结果很快出来了,大家解出的结果有很多个,下面是其中甲、乙两个同学的解法:
甲同学的解法:由f(1)=k+b,f(-1)=-k+b得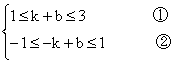
①+②得:0≤2b≤4,即0≤b≤2 ③
② ×(-1)+①得:-1≤k-b≤1 ④
④+②得:0≤2k≤4 ⑤
③+⑤得:0≤2k+b≤6。
又∵f(2)=2k+b
∴0≤f(2)≤6,0≤Z≤6
乙同学的解法是:由f(1)=k+b,f(-1)=-k+b得
①+②得:0≤2b≤4,即:0≤b≤2 ③
①-②得:2≤2k≤2,即:1≤k≤1
∴k=1,
∵f(2)=2k+b=1+b
由③得:1≤f(2)≤3
∴:1≤Z≤3
(Ⅰ)如果课堂上老师让你对甲、乙两同学的解法给以评价,你如何评价?
(Ⅱ)请你利用线性规划方面的知识,再写出一种解法。
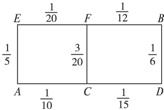 某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如如图所示.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为
某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如如图所示.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为| 1 |
| 10 |
| 1 |
| 15 |
 现在小型轿车慢慢进入百姓家庭,但是另一个问题相继暴露出来--堵车.李先生居住在城市的A处,准备开车到B处上班,若该地各路段发生堵车事件是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图所示(例如A→C→D并作两个路段:路段AC发生堵车事件的概率是
现在小型轿车慢慢进入百姓家庭,但是另一个问题相继暴露出来--堵车.李先生居住在城市的A处,准备开车到B处上班,若该地各路段发生堵车事件是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图所示(例如A→C→D并作两个路段:路段AC发生堵车事件的概率是| 1 |
| 10 |
| 1 |
| 15 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com