
题目列表(包括答案和解析)
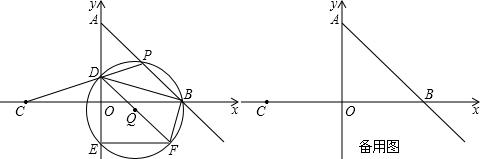
如图,在平面直角坐标系xoy中,抛物线y=![]() x 2-
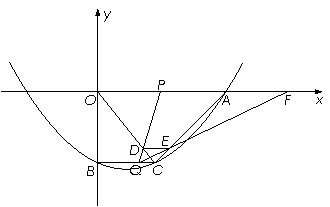
x 2-![]() x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
(1)求A,B,C三点的坐标和抛物线的顶点坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当t∈(0,![]() )时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
)时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
 |
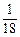 x2-
x2-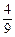 x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)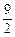 )时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
)时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;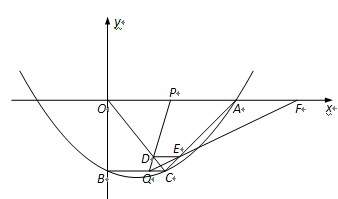
 (2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(1≤t≤
(2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(1≤t≤| 3 |
| 2 |
| 9 |
| 8 |
材料:为了美化环境,某房地产公司打算在所管辖的一个居民小区内的一块半圆形空地上,划出一个内接矩形辟为绿地,且使矩形的一边落在半圆的直径上,而另外两个顶点在半圆的圆周上,已知半圆的半径为30米.为了使绿地的面积最大,该公司请了本公司的一位设计师,设计出了这个半圆内接矩形的长与宽的关系.该设计师的计算过程如下:
如下图,设CD=x,则OD=![]() ,矩形的面积设为S,则
,矩形的面积设为S,则
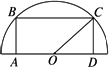
S=2x·![]() =
=![]() .
.
所以当x2=450,即x=![]() 时,S有最大值,即此时矩形的面积最大.
时,S有最大值,即此时矩形的面积最大.
问题:现在我们已经学习了三角函数的有关知识,利用三角函数的知识该如何解决这一问题?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com