查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

正△ABC的边长为4，CD是AB边上的高，E、F分别是AC和BC边的中点，现将△ABC沿CD翻折成直二面角A—DC—B。
(1)试判断直线AB与平面DEF的位置关系，并说明理由；
(2)求二面角E—DF—C的余弦值；
(3)在线段BC上是否存在一点P，使AP⊥DE？证明你的结论.

查看答案和解析>>

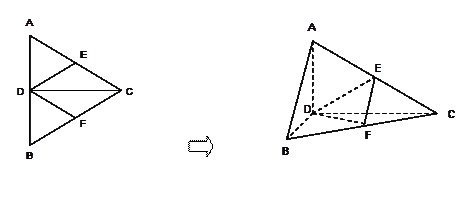
一、DDBCD  CABCA

二、11．1；       12．；     13．           14．；    15．；

16．

三．解答题（本大题共6小题，共76分）

17．解：（1）法一：由题可得；

法二：由题，

故，从而；

法三：由题，解得，

故，从而。

（2），令，

则，

在单调递减，

故，

从而的值域为。

18．解：（1）的可能取值为0,1,2,3,4，，

，

，，。

因此随机变量的分布列为下表所示；

0

1

2

3

4

（2）由⑴得：，

19．法一：（1）连接，设，则。

因为，所以，故，从而，

故。

又因为，

所以，当且仅当取等号。

此时为边的中点，为边的中点。

故当为边的中点时，的长度最小，其值为

（2）连接，因为此时分别为的中点，

故，所以均为直角三角形，

从而，所以即为直线与平面所成的角。

因为，所以即为所求；

（3）因，又，所以。

又，故三棱锥的表面积为

。

因为三棱锥的体积，

所以。

法二：（1）因，故。

设，则。

所以，

当且仅当取等号。此时为边的中点。

故当为的中点时，的长度最小，其值为；

（2）因，又，所以。

记点到平面的距离为，

因，故，解得。

因，故；

（3）同“法一”。

法三：（1）如图，以为原点建立空间直角坐标系，设，则，

所以，当且仅当取等号。

此时为边的中点，为边的中点。

故当为边的中点时，的长度最小，其值为；

（2）设为面的法向量，因，

故。取，得。

又因，故。

因此，从而，

所以；

（3）由题意可设为三棱锥的内切球球心，

则，可得。

与（2）同法可得平面的一个法向量，

又，故，

解得。显然，故。

20．解：（1）当时，。令得，

故当 时，单调递增；

当时，单调递减。

所以函数的单调递增区间为，

单调递减区间为；

（2）法一：因，故。

令，

要使对满足的一切成立，则，

解得；

法二：，故。

由可解得。

因为在单调递减，因此在单调递增，故。设，

则，因为，

所以，从而在单调递减，

故。因此，即。

（3）因为，所以

即对一切恒成立。

，令，

则。因为，所以，

故在单调递增，有。

因此，从而。

所以。

21．解：（1）设，则由题，

由得，故。

又根据可得，

即，代入可得，

解得（舍负）。故的方程为；

（2）法一：设，代入得，

故，

从而

因此。

法二：显然点是抛物线的焦点，点是其准线上一点。

设为的中点，过分别作的垂线，垂足分别为，

则。

因此以为直径的圆与准线相切（于点）。

若与重合，则。否则点在外，因此。

综上知。

22．证明：（1）因，故。

显然，因此数列是以为首项，以2为公比的等比数列；

（2）由⑴知，解得；

（3）因为

所以。

又（当且仅当时取等号），

故。

综上可得。（亦可用数学归纳法）