
题目列表(包括答案和解析)
(09年莱阳一中期末理)(12分)四棱锥![]() 中,
中,
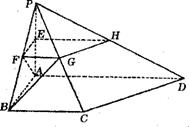
![]() ,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于F, G,H已知底面ABCD为直角梯形,AD∥BC,
,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于F, G,H已知底面ABCD为直角梯形,AD∥BC,![]() ,
,![]() 。
。
(1)求异面直线AF,BG所成的角的大小;
(2)设面APB与面CPD所成的锐二面角的大小为![]() ,求cos
,求cos![]() .
.
(满分12分)设底面边长为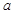 的正四棱柱
的正四棱柱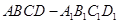 中,
中,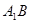 与平面
与平面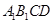 所成角为
所成角为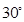 ;点
;点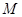 是棱
是棱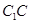 上一点.
上一点.

(1)求证:正四棱柱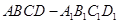 是正方体;
是正方体;
(2)若点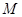 在棱
在棱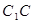 上滑动,求点
上滑动,求点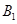 到平面
到平面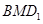 距离的最大值;
距离的最大值;
(3)在(2)的条件下,求二面角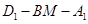 的大小.
的大小.
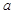 的正四棱柱
的正四棱柱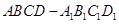 中,
中,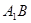 与平面
与平面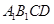 所成角为
所成角为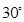 ;点
;点 是棱
是棱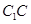 上一点.
上一点.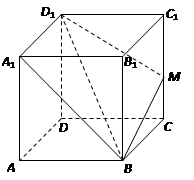
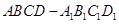 是正方体;
是正方体; 在棱
在棱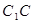 上滑动,求点
上滑动,求点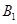 到平面
到平面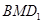 距离的最大值;
距离的最大值;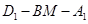 的大小.
的大小.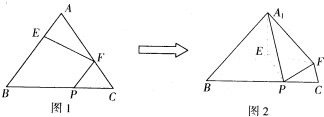 如图1,在正三角形ABC中,已知AB=5,E、F、P分别是AB、AC、BC边上的点,设
如图1,在正三角形ABC中,已知AB=5,E、F、P分别是AB、AC、BC边上的点,设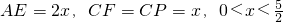 ,将△ABC沿EF折起到△A1EF的位置,使二面角A1-EF-B的大小为
,将△ABC沿EF折起到△A1EF的位置,使二面角A1-EF-B的大小为 ,连接A1B、A1P(如图2).
,连接A1B、A1P(如图2). ,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.
,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.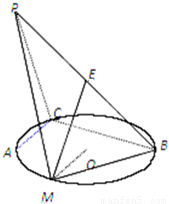
一.选择题:本大题共12小题,每小题5分,共60分。
(1)B (2)A (3)B (4)A (5)C (6)D
(7)A (8)C (9)B (10)A (11)D (12)B
二.填空题:本大题共4小题,每小题5分,共20分。
(13).files/image315.gif) (14)
(14).files/image317.gif) (15)
(15).files/image319.gif)
(16).files/image321.gif)
三.解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分10分)
(Ⅰ)解法一:由正弦定理得.files/image323.gif) .
.
故 .files/image325.gif) ,
,
又 .files/image327.gif) ,
,
故 .files/image329.gif) ,
,
即 .files/image331.gif) ,
,
故 .files/image333.gif) .
.
因为 .files/image335.gif) ,
,
故 .files/image337.gif) ,
,
又 .files/image202.gif) 为三角形的内角,
为三角形的内角,
所以
.files/image340.gif) . ………………………5分
. ………………………5分
解法二:由余弦定理得 .files/image342.gif) .
.
将上式代入.files/image206.gif) 整理得
整理得.files/image345.gif) .
.
故 .files/image337.gif) ,
,
又 .files/image202.gif) 为三角形内角,
为三角形内角,
所以 .files/image340.gif) .
………………………5分
.
………………………5分
(Ⅱ)解:因为.files/image348.gif) .
.
故 .files/image350.gif) ,
,
由已知 .files/image210.gif) 得
得
.files/image353.gif)
又因为 .files/image355.gif) .
.
得 .files/image357.gif) ,
,
所以
.files/image359.gif) ,
,
解得
.files/image361.gif) . ………………………………………………10分
. ………………………………………………10分
.files/image232.jpg) (18)(本小题满分12分)
(18)(本小题满分12分)
(Ⅰ)证明:
∵.files/image216.gif) 面
面.files/image214.gif) ,
,.files/image363.gif) 面
面.files/image214.gif) ,
,
∴.files/image366.gif) .
.
又∵底面.files/image214.gif) 是正方形,
是正方形,
∴.files/image368.gif) .
.
又∵.files/image370.gif) ,
,
∴.files/image372.gif) 面
面.files/image223.gif) ,
,
又∵.files/image363.gif) 面
面.files/image376.gif) ,
,
∴平面.files/image219.gif)
.files/image221.gif) 平面
平面.files/image223.gif) . ………………………………………6分
. ………………………………………6分
(Ⅱ)解法一:如图建立空间直角坐标系.files/image378.gif) .
.
设.files/image380.gif) ,则
,则.files/image382.gif) ,在
,在.files/image384.gif) 中,
中,.files/image386.gif) .
.
∴.files/image388.gif) 、
、.files/image390.gif) 、
、.files/image392.gif) 、
、.files/image394.gif) 、
、.files/image396.gif) 、
、.files/image398.gif) .
.
.files/image399.gif) ∵
∵.files/image128.gif) 为
为.files/image228.gif) 的中点,
的中点,.files/image401.gif) ,
,
∴.files/image403.gif) .
.
设.files/image405.gif) 是平面
是平面.files/image407.gif) 的一个法向量.
的一个法向量.
.files/image409.gif) 则由
则由.files/image411.gif) 可求得
可求得.files/image413.gif) .
.
由(Ⅰ)知.files/image415.gif) 是平面
是平面.files/image223.gif) 的一个法向量,
的一个法向量,
且.files/image418.gif) ,
,
∴.files/image420.gif) ,即
,即.files/image422.gif) .
.
∴二面角.files/image230.gif) 的大小为
的大小为.files/image424.gif) . ………………………………………12分
. ………………………………………12分
解法二:
.files/image426.jpg) 设
设.files/image380.gif) ,则
,则.files/image382.gif) ,
,
在.files/image384.gif) 中,
中,.files/image386.gif) .
.
设.files/image428.gif) ,连接
,连接.files/image430.gif) ,过
,过.files/image150.gif) 作
作.files/image433.gif) 于
于.files/image435.gif) ,
,
连结.files/image437.gif) ,由(Ⅰ)知
,由(Ⅰ)知.files/image439.gif) 面
面.files/image441.gif) .
.
∴.files/image437.gif) 在面
在面.files/image441.gif) 上的射影为
上的射影为.files/image444.gif) ,
,
∴.files/image446.gif) .
.
故.files/image448.gif) 为二面角
为二面角.files/image450.gif) 的平面角.
的平面角.
在.files/image452.gif) 中,
中,.files/image454.gif) ,
,.files/image456.gif) ,
,.files/image458.gif) .
.
∴.files/image460.gif) ,
,
∴.files/image462.gif) .
.
∴.files/image464.gif) .
.
即二面角.files/image230.gif) 的大小为
的大小为.files/image424.gif) . …………………………………12分
. …………………………………12分
(19)(本小题满分12分)
(Ⅰ)解:设.files/image200.gif) 、
、.files/image202.gif) 两项技术指标达标的概率分别为
两项技术指标达标的概率分别为.files/image289.gif) 、
、.files/image469.gif) .
.
由题意得:.files/image471.gif) …………2分
…………2分
∴.files/image473.gif) .
.
即一个零件经过检测为合格品的概率为.files/image164.gif) . …………6分
. …………6分
(Ⅱ)设该工人一个月生产的20件新产品中合格品有.files/image476.gif) 件,获得奖金
件,获得奖金.files/image478.gif) 元,则
元,则.files/image409.gif)
.files/image481.gif) . ………………8分
. ………………8分
.files/image483.gif) ~
~.files/image485.gif) ,
,.files/image487.gif) ,
………………10分
,
………………10分
.files/image489.gif) .
.
即该工人一个月获得奖金的数学期望是800元. ………………12分
(20)(本小题满分12分)
解:(Ⅰ)设双曲线方程为.files/image491.gif) ,
,.files/image493.gif) ,
,
由.files/image248.gif) ,
,.files/image250.gif) 及勾股定理得
及勾股定理得.files/image495.gif) ,
,
由双曲线定义得 .files/image497.gif) .
.
则.files/image499.gif) .
………………………………………5分
.
………………………………………5分
(Ⅱ).files/image501.gif) ,
,.files/image503.gif)
.files/image505.gif) ,故双曲线的两渐近线方程为
,故双曲线的两渐近线方程为.files/image507.gif) .
.
因为.files/image154.gif) 过
过.files/image252.gif) , 且
, 且.files/image258.gif) 与
与.files/image260.gif) 同向,故设
同向,故设.files/image154.gif) 的方程为
的方程为.files/image509.gif) ,
,
则.files/image511.gif)
又.files/image262.gif) 的面积
的面积.files/image513.gif) ,所以
,所以.files/image515.gif) .
.
可得.files/image154.gif) 与
与.files/image517.gif) 轴的交点为
轴的交点为.files/image519.gif) .
.
设.files/image154.gif) 与
与.files/image521.gif) 交于点
交于点.files/image200.gif) ,
,.files/image154.gif) 与
与.files/image524.gif) 交于点
交于点.files/image202.gif) ,
,
由.files/image527.gif) 得
得.files/image529.gif) ;由
;由.files/image531.gif) 得
得.files/image533.gif) .
.
故.files/image535.gif) ,
,
.files/image537.gif)
.files/image266.gif) ,
,.files/image503.gif)
.files/image540.gif) ,
,
从而.files/image542.gif) .
.
故.files/image268.gif) 的取值范围是
的取值范围是.files/image544.gif) . …………………………12分
. …………………………12分
(21)(本小题满分12分)
解:(Ⅰ).files/image546.gif) ,
,
.files/image548.gif) .
.
又因为函数.files/image274.gif) 在
在.files/image276.gif) 上为增函数,
上为增函数,
.files/image550.gif) 在
在.files/image276.gif) 上恒成立,等价于
上恒成立,等价于
.files/image552.gif) 在
在.files/image276.gif) 上恒成立.
上恒成立.
又.files/image554.gif) ,
,
故当且仅当.files/image556.gif) 时取等号,而
时取等号,而.files/image558.gif) ,
,
.files/image560.gif) 的最小值为
的最小值为.files/image562.gif) .
………………………………………6分
.
………………………………………6分
(Ⅱ)由已知得:函数.files/image270.gif) 为奇函数,
为奇函数,
.files/image564.gif) ,
, .files/image566.gif) , ………………………………7分
, ………………………………7分
.files/image568.gif) .
.
.files/image537.gif) 切点为
切点为.files/image571.gif) ,其中
,其中.files/image573.gif) ,
,
则切线.files/image154.gif) 的方程为:
的方程为:.files/image575.gif) ……………………8分
……………………8分
由.files/image577.gif) ,
,
得.files/image579.gif) .
.
又.files/image581.gif) ,
,
.files/image583.gif) ,
,
.files/image585.gif) ,
,
.files/image587.gif) ,
,
.files/image589.gif) 或
或.files/image591.gif) ,由题意知,
,由题意知,.files/image593.gif)
从而.files/image595.gif) .
.
.files/image597.gif) ,
,
.files/image599.gif) ,
,
.files/image601.gif) .
………………………………………12分
.
………………………………………12分
(22)(本小题满分12分)
(Ⅰ)解: 由.files/image603.gif) ,
,.files/image605.gif)
.files/image301.gif) 得
得
.files/image607.gif) ,
,.files/image609.gif) . …………………………3分
. …………………………3分
(Ⅱ)由(Ⅰ)归纳得.files/image611.gif)
.files/image613.gif) , ………………………4分
, ………………………4分
用数学归纳法证明:
①当.files/image615.gif) 时,
时,.files/image605.gif) 成立.
成立.
②假设.files/image618.gif) 时,
时,.files/image620.gif) 成立,
成立,
那么.files/image622.gif)
.files/image301.gif)
所以当.files/image624.gif) 时,等式也成立.
时,等式也成立.
由①、②得.files/image611.gif)
.files/image301.gif) 对一切
对一切.files/image627.gif) 成立. ……………8分
成立. ……………8分
(Ⅲ)证明: 设.files/image629.gif) ,则
,则.files/image631.gif) ,
,
所以.files/image633.gif) 在
在.files/image635.gif) 上是增函数.
上是增函数.
故.files/image637.gif) .
.
即.files/image639.gif) .
.
因为.files/image641.gif) ,
,
故.files/image643.gif) .
.
.files/image645.gif) =
=.files/image647.gif) .…………12分
.…………12分
本资料由《七彩教育网》www.7caiedu.cn 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com