
题目列表(包括答案和解析)
| OA |
| BA |
| OB |
| A、椭圆 | B、双曲线 | C、抛物线 | D、圆 |
| OA |
| BA |
| OB |
| A.椭圆 | B.双曲线 | C.抛物线 | D.圆 |
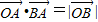 (O为坐标原点),则动点A的轨迹是( )
(O为坐标原点),则动点A的轨迹是( )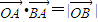 (O为坐标原点),则动点A的轨迹是( )
(O为坐标原点),则动点A的轨迹是( )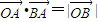 (O为坐标原点),则动点A的轨迹是( )
(O为坐标原点),则动点A的轨迹是( )一、选择题:本大题共12小题,每题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.B 2.C 3.B 4.D 5.C 6.D 7.D 8.B 9.A 10.B 11.A 12.
二、填空题:本大题共4小题,每小题5分
13.27 14.20 15.2 16.①④
三、解答题(解答应写出文字说明,证明过程或演算步骤)
17.(本小题共10分)
解:(I).files/image212.gif)
.files/image214.gif)
故函数.files/image114.gif) 的周期为
的周期为.files/image217.gif) ………………………………………….5分
………………………………………….5分
(II).files/image219.gif)
又.files/image221.gif)
.files/image223.gif)
.files/image225.gif) 函数
函数.files/image169.gif) 的值域为
的值域为.files/image228.gif) ………………….10分
………………….10分
18.(本小题共12分)
解:(1)3名志愿者每人任选一天参加社区服务,共有53种不同的结果,这些结果出现的可能性都相等. ………………1分
设“3名志愿者恰好连续3天参加社区服务工作”为事件A,
则该事件共包括.files/image230.gif) 种不同的结果, ………………3分
种不同的结果, ………………3分
所以.files/image232.gif) ………………5分
………………5分
答:3名志愿者恰好连续3天参加社区服务工作的概率为.files/image234.gif) ………………6分
………………6分
(II)解法1:随机变量ξ的可能取值为0,1,2,3 ………………7分
.files/image236.gif)
随机变量ξ的分布列为:
ξ
0
1
2
3
P
.files/image238.gif)
.files/image240.gif)
.files/image242.gif)
.files/image244.gif)
……………………12分
解法2:每名志愿者在5月1日参加社区服务的概率均为.files/image246.gif) ……7分
……7分
则三名志愿者在5月1日参加社区服务的人数.files/image248.gif)
.files/image250.gif) ………………11分
………………11分
随机变量ξ的分布列为:
ξ
0
1
2
3
P
.files/image238.gif)
.files/image240.gif)
.files/image242.gif)
.files/image244.gif)
………………12分
19.(本小题共12分)
方法1
(I)证明:在直角梯形ABCD中,∵AB//CD,∠BAD=90°,AD=DC=2
∴∠ADC=90°,且.files/image252.gif) ………………1分
………………1分
取AB的中点E,连结CE.
由题意可知,四边形AECD为正方形,所以AE=CE=2,
又.files/image254.gif)
则△ABC为等腰直角三角形,
所以AC⊥BC, 又因为PA⊥平面ABCD,则AC为PC在平面ABCD内的射影,BC.files/image256.gif) 平面ABCD,
平面ABCD,
由三垂线定理得,BC⊥PC ……………………4分
(II)由(I)可知,BC⊥PC,BC⊥AC,PC∩AC=C.
所以BC⊥平面PAC, ……………………4分
PC是PB在平面APC内的射影,所以∠CPB是PB与平面PAC所成的角. ……5分
又.files/image258.gif) , ………………6分
, ………………6分
.files/image260.gif) ………………7分
………………7分
.files/image262.gif) ………………8分
………………8分
(III)由(II)可知,BC⊥平面PAC,BC.files/image256.gif) 平面PEC,
平面PEC,
所以平面PBC⊥平面PAC,
过A点在平面PAC内作AF⊥PC于E,所以AF⊥平面PBC,
则AF的长即为点A到平面PBC的距离. ………………9分
在直角三角形PAC中,PA=2,AC=.files/image265.gif) , ………………10分
, ………………10分
.files/image267.gif) ………………11分
………………11分
所以.files/image269.gif) ………………12分
………………12分
方法2:
∵AP⊥平面ABCD,∠BAD=90°
∴以A为原点,AD、AB、AP分别为x、y、z轴,建立空间直角坐标系
∵PA=AD=DC=2,AB=4.
.files/image271.gif) ………………2分
………………2分
(I).files/image273.gif)
.files/image275.gif) ………………3分
………………3分
.files/image277.gif) ………………4分
………………4分
(II).files/image279.gif)
.files/image281.gif)
设.files/image283.gif) ………………6分
………………6分
.files/image285.gif)
.files/image287.gif)
即PB与平面PAC所成角的正弦值为.files/image289.gif) ………………8分
………………8分
(III)由.files/image291.gif)
.files/image293.gif)
设.files/image295.gif) ………………10分
………………10分
.files/image297.gif) =
=.files/image299.gif)
∴点A到平面PBC的距离为.files/image299.gif) ………………12分
………………12分
20.(本小题共12分)
解:(I)令.files/image301.gif) ,得
,得.files/image303.gif) (舍去负的),
(舍去负的),
.files/image305.gif)
同理,令.files/image307.gif) 可得
可得.files/image309.gif) ................................................4分
................................................4分
(II).files/image311.gif)
.files/image313.gif) …………………8分
…………………8分
(Ⅲ)令.files/image315.gif)
.files/image317.gif)
.files/image319.gif)
.files/image321.gif)
.files/image323.gif) ………………..12分
………………..12分
21.(本小题共12分)
解:(I)由.files/image325.gif)
.files/image327.gif)
当.files/image202.gif) 时,
时,.files/image330.gif) 当
当.files/image332.gif) 时,
时,.files/image334.gif) ,
,
.files/image336.gif)
.files/image338.gif) 的单调递增区间是(-1,0),单调递减区间是(0,
的单调递增区间是(-1,0),单调递减区间是(0,.files/image340.gif) )….6分
)….6分
(II)设.files/image342.gif)
则.files/image344.gif)
当.files/image346.gif) 时,
时,.files/image348.gif) 在
在.files/image350.gif) 上是减函数;
上是减函数;
当.files/image352.gif) 时,
时,.files/image354.gif) 在
在.files/image356.gif) 上是增函数。
上是增函数。
.files/image358.gif)
.files/image360.gif) ………………………………………………………..12分
………………………………………………………..12分
22.(本小题共12分)
解:(I)如图,由题意得,.files/image362.gif)
.files/image364.gif)
∴所求的椭圆方程为.files/image366.gif) ………………3分
………………3分
.files/image372.gif)
(III)设.files/image374.gif)
若以MP为直径的圆恒过DP,MQ的交点,
则.files/image376.gif) 恒成立. ………………10分
恒成立. ………………10分
由(II)可知.files/image378.gif) ………………10分
………………10分
.files/image380.gif)
∴存在Q(0,0),使得以MP为直径的圆恒过直线DP,MQ的交点. …………12分
本资料由《七彩教育网》www.7caiedu.cn 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com