
题目列表(包括答案和解析)
老师给出一个函数,请三位同学各说出了这个函数的一条性质:
①此函数为偶函数;
②定义域为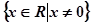 ;
;
③在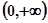 上为增函数.
上为增函数.
老师评价说其中有一个同学的结论错误,另两位同学的结论正确。请你写出一个(或几个)这样的函数
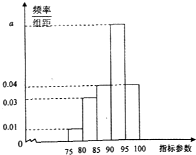 (2012•衡阳模拟)针对频繁发生的校车事故,2011年12月27日,工信部发布公告,公开征求对新制订的有关校车安全的几个条例的意见,我市为了了解实际情况,随机抽取了 100辆校车进行检测,将这些校车检測的某项指标参数绘制成如图所示的频率分布直方图.
(2012•衡阳模拟)针对频繁发生的校车事故,2011年12月27日,工信部发布公告,公开征求对新制订的有关校车安全的几个条例的意见,我市为了了解实际情况,随机抽取了 100辆校车进行检测,将这些校车检測的某项指标参数绘制成如图所示的频率分布直方图.| AM |
| BM |
| 2π | 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com