
题目列表(包括答案和解析)
| 数学成绩 | 90分以下 | 90-120分 | 120-140分 | 140分以上 |
| 频 数 | 15 | 20 | 10 | 5 |
| 数学成绩 | 90分以下 | 90-120分 | 120-140分 | 140分以上 |
| 频 数 | 5 | 40 | 3 | 2 |
| 班 次 | 120分以下(人数) | 120分以上(人数) | 合计(人数) |
| 一班 | |||
| 二班 | |||
| 合计 |
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 |
 (2009•宁波模拟)某市十所重点中学进行高三联考,共有5000名考生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如图所示的频率分布直方图.据此估计全体考生中120分及以上的学生数为
(2009•宁波模拟)某市十所重点中学进行高三联考,共有5000名考生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如图所示的频率分布直方图.据此估计全体考生中120分及以上的学生数为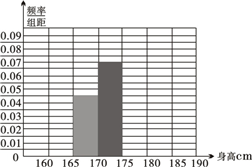 (2012•江西模拟)某省重点中学从高二年级学生中随机地抽取120名学生,测得身高情况如下表所示.
(2012•江西模拟)某省重点中学从高二年级学生中随机地抽取120名学生,测得身高情况如下表所示.| 分组 | 频数 | 频率 |
| [160,165) | 6 | 0.05 |
| [165,170) | 27 | 0.225 |
| [170,175) | 42 | ② |
| [175,180) | 36 | 0.3 |
| [180,185) | ① | 0.05 |
| [185,180) | 3 | 0.0258 |
| 合计 | 120 | 1 |
 杨辉是中国南宋末年的一位杰出的数学家、数学教育家,他的数学研究与教育工作的重点是在计算技术方面,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关.图是一个7阶的杨辉三角.
杨辉是中国南宋末年的一位杰出的数学家、数学教育家,他的数学研究与教育工作的重点是在计算技术方面,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关.图是一个7阶的杨辉三角.| (n+1)2 | 2 |
| 分组 | 频数 | 频率 | |
| 一 | 60.5~70.5 | A | 0.26 |
| 二 | 70.5~80.5 | 15 | C |
| 三 | 80.5~90.5 | 18 | 0.36 |
| 四 | 90.5~100.5 | B | D |
| 合计 | 50 | E | |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com