
题目列表(包括答案和解析)
| 4 | 3 |
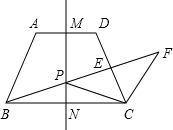 的对称轴,点P是线段MN上一个动点(不与M、N重合),射线BP交线段CD于点E,过点C作CF∥AB交射线BP于点F.
的对称轴,点P是线段MN上一个动点(不与M、N重合),射线BP交线段CD于点E,过点C作CF∥AB交射线BP于点F.
书本P58实验与探究中,介绍了三角形中边与角之间的不等关系,利用轴对称方法证明了:一个三角形中,如果两条边不等,那么它们所对的角也不等,大边所对的角较大。
下面用另外一种方法来证明这个结论。
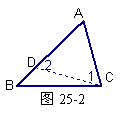
如图25-1,在⊿ABC中,AB>AC,求证:∠ACB>∠B
证明:如图25-2,在边AB截取一点D,使AD=AC, ∵AD=AC ∴∠1=∠2
∴∠ACB>∠1 又∵∠1=∠2 ∠2>∠B ∴∠ACB>∠B
利用上述结论或方法,解决下列问题:
(1)在⊿ABC中,已知BC>AB>AC,猜想∠A,∠B,∠C的大小关系是_________________
(2)已知:如图25-3,在⊿ABC中,∠ACB>∠B,求证:AB>AC
(3)如果一![]() 个三角形中最大的边所对的角是锐
个三角形中最大的边所对的角是锐![]() 角,这个三角形一定是锐角三角形吗?为什么?
角,这个三角形一定是锐角三角形吗?为什么?

 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com