（本小题满分10分）

    学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.

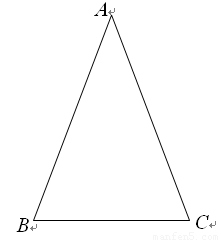
类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=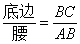.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.

根据上述对角的正对定义，解下列问题：

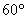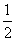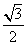（1）sad 的值为（   ）A.       B. 1  C.      D. 2

（2）对于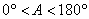，∠A的正对值sad A的取值范围是         .

（3）已知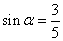，其中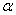为锐角，试求sad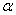的值.

（本小题满分5分）

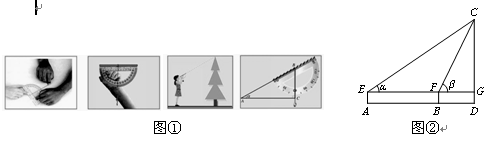
小红在学习了教科书上相关内容后自制了一个测角仪（图①），并尝试用它来测量校园内一座教学楼CD的高度（如图②）.她先在A处测得楼顶C的仰角30°，再向楼的方向直行10米到达B处，又测得楼顶C的仰角60°，若小红的目高（眼睛到地面的高度）AE为1.60米，请你帮助她计算出这座教学楼CD的高度（结果精确到0.1米，参考数据：，，）.

（本小题满分10分）

在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：

第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图1）；

第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）

请解答以下问题：

1.（1）如图2，若延长MN交BC于P，△BMP是什么三角形？请证明你的结论．

2.（2）在图2中，若AB=a，BC=b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP ？

(本小题满分8分)

学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计.图(1)和图(2)是    他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问 题:

 1. (1)求该班共有多少名学生?

 2. (2)在图（1）中,将表示“步行”的部分补充完整；

 3.  (3)在扇形统计图中，计算出“骑车”部分所对应的圆心角的度数；

 4. (4)如果全年级共600名同学,请你估算全年级步行上学的学生人数？