
题目列表(包括答案和解析)
过抛物线

 的对称轴上的定点
的对称轴上的定点 ,作直线
,作直线 与抛物线相交于
与抛物线相交于 两点.
两点.
(I)试证明 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(II)若点 是定直线
是定直线 上的任一点,试探索三条直线
上的任一点,试探索三条直线 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.
【解析】本题主要考查抛物线与直线的位置关系以及发现问题和解决问题的能力.
(1)中证明:设 下证之:设直线AB的方程为: x=ty+m与y2=2px联立得消去x得y2=2pty-2pm=0,由韦达定理得
下证之:设直线AB的方程为: x=ty+m与y2=2px联立得消去x得y2=2pty-2pm=0,由韦达定理得

(2)中:因为三条直线AN,MN,BN的斜率成等差数列,下证之
设点N(-m,n),则直线AN的斜率KAN= ,直线BN的斜率KBN=
,直线BN的斜率KBN=

KAN+KBN= +
+
本题主要考查抛物线与直线的位置关系以及发现问题和解决问题的能力.
 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
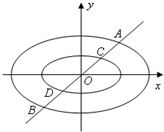 定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:| x2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
 定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆 .
.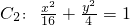 ,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由;
,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由; 和
和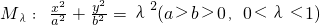 分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明) .
. ,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由;
,判断C2与C1是否相似?如果相似,求出C2与C1的相似比;如果不相似,请说明理由; 和
和 分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
分别交于点A,B和点C,D,试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点),使△CDF和△ABE组成以λ为相似比的两个相似三角形,写出具体作法.(不必证明)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com