
题目列表(包括答案和解析)
若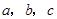 是不全相等的实数,求证:
是不全相等的实数,求证: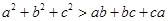 .
.
证明过程如下:
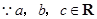 ,
,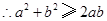 ,
,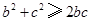 ,
,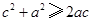 ,
,
又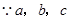 不全相等,
不全相等,
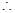 以上三式至少有一个“
以上三式至少有一个“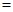 ”不成立,
”不成立,
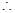 将以上三式相加得
将以上三式相加得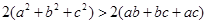 ,
,
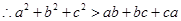 .
.
此证法是( )
A.分析法 B.综合法 C.分析法与综合法并用 D.反证法
若a,b,c是不全相等的实数,求证:a2+b2+c2>ab+bc+ca.
证明过程如下:
∵a、b、c∈R,∴a2+b2≥2ab,
b2+c2≥2bc,c2+a2≥2ac,
又∵a,b,c不全相等,
∴以上三式至少有一个“=”不成立,
∴将以上三式相加得2(a2+b2+c2)>2(ab+bc+ac),
∴a2+b2+c2>ab+bc![]() +ca.
+ca.
此证法是( )
(A)分析法 (B)综合法
(C)分析法与综合法并用 (D)反证法
老师给出一个函数,四个学生甲、乙、丙、丁各指出这个函数的一个性质:
甲:对于任意x∈R,都有f(1+x)=f(1-x);
乙:在(-∞,0]上,函数f(x)单调递减;
丙:在(0,+∞)上,函数f(x)单调递增;
丁:f(0)不是函数f(x)的最小值。
如果其中有三个人说得正确,则这个函数f(x)的解析式可能是_______。
老师给出一个函数,四个学生甲、乙、丙、丁各指出这个函数的一个性质:
甲:对于任意x∈R,都有f(1+x)=f(1-x);
乙:在(-∞,0]上,函数f(x)单调递减;
丙:在(0,+∞)上,函数f(x)单调递增;
丁:f(0)不是函数f(x)的最小值。
如果其中有三个人说得正确,则这个函数f(x)的解析式可能是_______。
设椭圆 (常数
(常数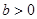 )的左右焦点分别为
)的左右焦点分别为 ,
, 是直线
是直线 上的两个动点,
上的两个动点, .
.
(1)若 ,求
,求 的值;
的值;
(2)求 的最小值.
的最小值.

【解析】第一问中解:设 ,
, 则
则
由 得
得 由
由 ,得
,得
 ②
②

第二问易求椭圆 的标准方程为:
的标准方程为:
 ,
,
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .
.
解:设 ,
, ……………………1分
……………………1分
则 ,由
,由 得
得 ①……2分
①……2分
(1)由 ,得
,得 ② ……………1分
② ……………1分
 ③ ………………………1分
③ ………………………1分
由①、②、③三式,消去 ,并求得
,并求得 .
………………………3分
.
………………………3分
(2)解法一:易求椭圆 的标准方程为:
的标准方程为: .………………2分
.………………2分
 , ……4分
, ……4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .…2分
.…2分
解法二: ,
………………4分
,
………………4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com