
题目列表(包括答案和解析)
| 1 |
| 2^ |
| 3 |
| 2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 5 |
| 3 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 7 |
| 4 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (n+1)2 |
| 2n-1 |
| n2 |
| 2n-1 |
| n2 |
如图是见证魔术师“论证”64=65的神奇.对这个乍看起来颇为神秘的现象,我们运用数学知识不难发现其中的谬误.另外,我们可以更换图中的数据,就能构造出许多更加直观与“令人信服”的“论证”.现请你用数列知识归纳:(1)这些图中的数所构成的数列:________;
(2)写出与这个魔术关联的一个数列递推关系式:________.

我们在数学必修1学习《集合与函数概念》时,可得本章知识结构大致如下:
据下图试分析本章知识结构.

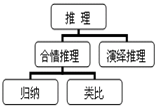 如图是《推理》知识结构框图,根据该框图可得
如图是《推理》知识结构框图,根据该框图可得 如图是《推理》知识结构框图,根据该框图可得
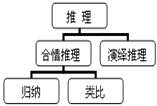
(1) “推理”主要包括两部分内容
(2) 知道“推理”概念后,只能进行“合情推理”内容的学习
(3) “归纳”与“类比”都不是演绎推理
(4) 可以先学习“类比”再学习“归纳”
这些命题
(A) 除(2)外都正确 (B) 除(3)外都正确
C) (1)(4)正确 (D) 全部正确
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com