练习册

  • 练习册
  • 试题
    常见图像变化规律:(注意平移变化能够用向量的语言解释.和按向量平移联系起来思考) 平移变换 y=f+b 注意:(ⅰ)有系数.要先提取系数.如:把函数y＝f(2x)经过 平移得到函数y＝f的图象. (ⅱ)会结合向量的平移.理解按照向量(m.n)平移的意义. 对称变换 y=f,关于y轴对称 y=f ,关于x轴对称 y=f(x)→y=f|x|,把x轴上方的图象保留.x轴下方的图象关于x轴对称 y=f|把y轴右边的图象保留.然后将y轴右边部分关于y轴对称. 伸缩变换:y=f, y=f具体参照三角函数的图象变换. 一个重要结论:若f.则函数y=f(x)的图像关于直线x=a对称, 【查看更多】

     

    题目列表(包括答案和解析)

    某研究性学习小组研究函数y＝lnx上的点P(x，y)与原点O的连线所在的直线的斜率k的值的变化规律．记直线OP的斜率k＝f(x)．

    (Ⅰ)某同学甲发现：点P从左向右运动时，f(x)不断增大，试问：他的判断是否正确？若正确，请说明理由：若不正确，请给出你的正确判断；

    (Ⅱ)某同学乙发现：总存在正实数a、b(a＜b)，使ab＝ba．试问：他的判断是否正确？若不正确，请说明理由：若正确，请求出a的取值范围；

    (Ⅲ)某同学丙发现：当x＞0时，函数k＝f(x)的图像总在函数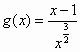的图像的下方，试问：他的判断是否正确？若正确，请说明理由：若不正确，请给出你的正确判断；

    查看答案和解析>>

    若函数y=f(x)是以T为周期的周期函数，请写出函数y=f(x)的函数值的变化规律和图像特征．

    查看答案和解析>>

    根据图中5个图形及相应点的个数的变化规律，试猜测第8个图中有
    57
    57
    个点．

    查看答案和解析>>

    根据图中5个图形及相应点的个数的变化规律，试猜测第6个图中有
    31
    31
    个点．

    查看答案和解析>>

    某“海之旅”表演队在一海滨区域进行集训，该海滨区域的海浪高度y（米）随着时间t（0≤t≤24，单位：小时）而周期性变化．为了了解变化规律，该队观察若干天后，得到每天各时刻t的浪高数据的平均值如下表：
    t（时） 0 3 6 9 12 15 18 21 24
    y（米） 1，0 1，4 1，0 0，6 1，0 1，4 0，9 0，4 1，0
    （Ⅰ）可近似地看成是函数y=Asin（ωt+φ）+b求出该拟合模型的解析式；
    （Ⅱ）如果确定当浪高不低于0.8米时才进行训练，试安排白天内进行训练的具体时间段．

    查看答案和解析>>


    同步练习册答案