
题目列表(包括答案和解析)
(06年广东卷)(15分)(1)人们发现光电效应具有瞬时性和对各种金属都存在极限频率的规律。请问谁提出了何种学说很好地解释了上述规律?已知锌的逸出功为3.34e,用某单色紫外线照射锌板时,逸出光电子的最大速度为106m/s,求该紫外线的波长λ(电子质量me=9.11×![]() kg
kg![]() J?s,1eV=1.6×10
J?s,1eV=1.6×10![]() J)。
J)。
(2)风力发电是一种环保的电能获取方式。图9为某风力发电站外观图。设计每台风力发电机的功率为40kW。实验测得风的动能转化为电能的效率约为20%,空气的密度是1.29kg/m3,当地水平风速约为10m/s,问风力发电机的叶片长度约为多少才能满足设计要求?
(06年广东卷)(14分)一个质量为![]() 的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数
的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数![]() 。从
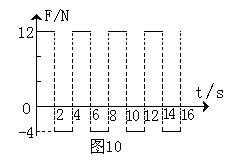
。从![]() 开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图10所示。求83秒内物体的位移大小和力F对物体所做的功。
开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图10所示。求83秒内物体的位移大小和力F对物体所做的功。![]() 取
取![]() 。
。
(06年广东卷)(16分)宇宙中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行。设每个星体的质量均为![]() 。
。
(1)试求第一种形式下,星体运动的线速度和周期。
(2)假设两种形式星体的运动周期相同,第二种形式下星体之间的距离应为多少?
(06年全国卷Ⅰ)我国将要发射一颗绕月运行的探月卫星“嫦娥1号”。设该卫星的轨道是圆形的,且贴近月球表面。已知月球的质量约为地球质量的1/81,月球的半径约为地球半径的1/4,地球上的第一宇宙速度约为7.9 km/s,则该探月卫星绕月运行的速率约为
A. 0.4 km/s B. 1.8 km/s C. 11 km/s D. 36 km/s
(06年四川卷)(16分)荡秋千是大家喜爱的一项体育运动。随着科技迅速发展,将来的某一天,同学们也会在其它星球上享受荡秋千的乐趣。假设你当时所在星球的质量是M、半径为R,可将人视为质点,秋千质量不计、摆长不变、摆角小球90°,万有引力常量为G。那么,
(1)该星球表面附近的重力加速度![]() 等于多少?
等于多少?
(2)若经过最低位置的速度为v0,你能上升的最大高度是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com