
题目列表(包括答案和解析)
 ]上的函数y=f(x)的图象关于直线x=
]上的函数y=f(x)的图象关于直线x= 对称,当x
对称,当x 时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为( )
时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为( )


 ]上的函数y=f(x)的图象关于直线x=
]上的函数y=f(x)的图象关于直线x= 对称,当x
对称,当x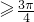 时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为
时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为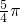


已知定义在区间[-p,![]() ] 上的函数y=f(x)的图象关于直线x= -
] 上的函数y=f(x)的图象关于直线x= -![]() 对称,当xÎ[-
对称,当xÎ[-![]() ,
,![]() ]时,函数f(x)=Asin(wx+j)(A>0, w>0,-
]时,函数f(x)=Asin(wx+j)(A>0, w>0,-![]() <j<
<j<![]() ),其图象如图所示。
),其图象如图所示。
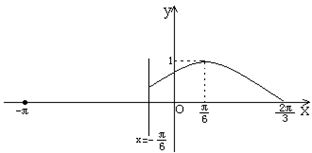 (1)求函数y=f(x)在[-p,
(1)求函数y=f(x)在[-p,![]() ]的表达式;
]的表达式;
(2)求方程f(x)=![]() 的解。
的解。
已知定义在区间[-p,![]() ]上的函数y=f(x)的图象关于直线x=-
]上的函数y=f(x)的图象关于直线x=-![]() 对称,当x
对称,当x![]() [-
[-![]() ,
,![]() ]时,函数f(x)=Asin(wx+j)(A>0, w>0,-
]时,函数f(x)=Asin(wx+j)(A>0, w>0,-![]() <j<
<j<![]() ),其图象如图所示。
),其图象如图所示。
(1)求函数y=f(x)在[-p,![]() ]的表达式;
]的表达式;
(2)求方程f(x)=![]() 的解。
的解。

已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论:
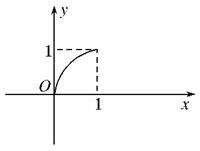
①f(x2)-f(x1)>x2-x1;
②x2f(x1)>x1f(x2);
③![]() <f
<f![]() .
.
其中正确结论的序号是___: _____.(把所有正确结论的序号都填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com