
题目列表(包括答案和解析)
(本小题满分12分)二次函数![]() 的图象经过三点
的图象经过三点![]() .
.![]()
(1)求函数![]() 的解析式(2)求函数
的解析式(2)求函数![]() 在区间
在区间![]() 上的最大值和最小值
上的最大值和最小值
(本小题满分12分)已知等比数列{an}中,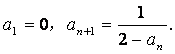
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设数列{an}的前n项和为Sn,证明:![]() ;
;
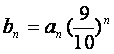 ,证明:对任意的正整数n、m,均有
,证明:对任意的正整数n、m,均有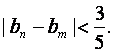
(本小题满分12分)已知函数![]() ,其中a为常数.
,其中a为常数.
(Ⅰ)若当![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
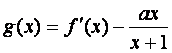 的单调区间.
的单调区间.(本小题满分12分)
甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为![]() ,乙投篮命中的概率为
,乙投篮命中的概率为![]()
(Ⅰ)求甲至多命中2个且乙至少命中2个的概率;
(Ⅱ)若规定每投篮一次命中得3分,未命中得-1分,求乙所得分数η的概率分布和数学期望.(本小题满分12分)已知![]() 是椭圆
是椭圆![]() 的两个焦点,O为坐标原点,点
的两个焦点,O为坐标原点,点![]() 在椭圆上,且
在椭圆上,且![]() ,圆O是以
,圆O是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与圆O相切,并且与椭圆交于不同的两点A、B.
与圆O相切,并且与椭圆交于不同的两点A、B.
(1)求椭圆的标准方程;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)当![]() 时,求弦长|AB|的取值范围.
时,求弦长|AB|的取值范围.
一、选择题
1-6 C A B B B D 7-12 B C B B B C
二、填空
13. 4 14. .files/image195.gif) 15. 2 16.
15. 2 16..files/image197.gif)
三、解答题
17.(1)解:由.files/image199.gif)
有.files/image201.gif) ……6分
……6分
由.files/image203.gif) , ……8分
, ……8分
由余弦定理.files/image205.gif)
当.files/image207.gif) ……12分
……12分
.files/image208.jpg) ∴PB∥平面EFG. ………………………………3分
∴PB∥平面EFG. ………………………………3分
(2)解:取BC的中点M,连结GM、AM、EM,则GM//BD,
|