练习册

  • 练习册
  • 试题
    ABCD为正方形.△PAD是直角三角形.且PA=AD=2.E.F.G分别是线段PA.PD.CD的中点. 1,3,5 (2)求异面直线EG与BD所成的角, (3)在线段CD上是否存在一点Q.使得A点到平面 【查看更多】

     

    题目列表(包括答案和解析)

    如图，平面PAD⊥平面ABCD，ABCD为正方形，△PAD是直角三角形，且PA=AD=2，E、F、G分别是线段PA、PD、CD的中点．
    （1）求证：面EFG⊥面PAB；
    （2）求异面直线EG与BD所成的角；
    （3）求点A到面EFG的距离．

    查看答案和解析>>

    如图，平面PAD⊥平面ABCD，ABCD为正方形，△PAD是直角三角形，且PA=AD=2，E、F、G分别是线段PA、PD、CD的中点．
    （1）求证：面EFG⊥面PAB；
    （2）求异面直线EG与BD所成的角；
    （3）求点A到面EFG的距离．

    查看答案和解析>>

    如图，平面PAD⊥平面ABCD，ABCD为正方形，△PAD是直角三角形，且PA=AD=2，E、F、G分别是线段PA、PD、CD的中点．
    （1）求证：面EFG⊥面PAB；
    （2）求异面直线EG与BD所成的角；
    （3）求点A到面EFG的距离．

    查看答案和解析>>

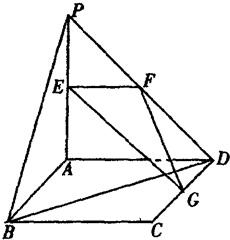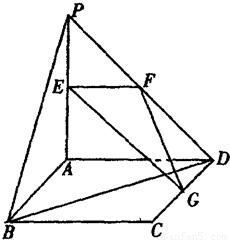
    如图，平面PAD⊥平面ABCD，ABCD为正方形，△PAD是直角三角形，且PA＝AD＝2，E、F、G分别是线段PA，PD，CD的中点．

    (1)求证：PB∥面EFG；

    (2)求异面直线EG与BD所成的角；

    (3)在线段CD上是否存在一点Q，使得点A到平面EFQ的距离为0.8．若存在，求出CQ的值；若不存在，请说明理由．

    查看答案和解析>>

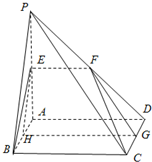    如图，平面PAD⊥平面ABCD，四边形ABCD为正方形，△PAD是直角三角形，且PA=AD=2，E，F，G，H分别是线段PA，PD，CD，AB的中点．
    （Ⅰ）求证：PB∥平面EFGH；
    （Ⅱ）求二面角C-EF-G的余弦值．

    查看答案和解析>>

    一、选择题

     1-6  C  A  B  B   B   D    7-12   B  C  B  B  B  C

    二、填空 

     13．  4     14．      15． 2    16．

    三、解答题

    17．（1）解：由

           有    ……6分

    由，  ……8分

    由余弦定理

          当……12分

    ∴PB∥平面EFG. ………………………………3分

       （2）解：取BC的中点M，连结GM、AM、EM，则GM//BD，

    所成的角.………………4分

         在Rt△MAE中， ，

         同理，…………………………5分

    又GM=，

    ∴在△MGE中，

    ………………6分

    故异面直线EG与BD所成的角为arccos，………………………………7分

       （3）假设在线段CD上存在一点Q满足题设条件，

    ∵ABCD是正方形，△PAD是直角三角形，且PA=AD=2，

    ∴AD⊥AB，AD⊥PA.

    又AB∩PA=A,

    ∴AD⊥平面PAB. ……………………………………8分

    又∵E，F分别是PA，PD中点，

    ∴EF∥AD，∴EF⊥平面PAB.

    又EF面EFQ，

    ∴面EFQ⊥面PAB. …………………………………9分

    过A作AT⊥ER于T，则AT⊥平面EFQ，

    ∴AT就是点A到平面EFQ的距离. ……………………………………………10分

    设，

        在， …………………………11分

        解得

        故存在点Q，当CQ=时，点A到平面EFQ的距离为0.8. ……………………… 12分

    解法二：建立如图所示的空间直角坐标系A－xyz，

    则A（0，0，0），B（2，0，0），C（2，2，0），D（0，2，0），

       （1）证明：

         …………………………1分

        设，

        即，

       

         ……………2分

        ，

        ∴PB∥平面EFG. …………………………………………………………………… 3分

       （2）解：∵,…………………………………………4分

        ，……………………… 6分

     

    20．（本小题满分12分）

    解：（1）数列{an}的前n项和，

                                          …………2分

    又，

                               …………3分

    是正项等比数列，

     

    ，                                               …………4分

    公比，                                                                                    …………5分

    数列                                  …………6分

       （2）解法一：，

    由                        …………8分

    ，

    当，                                      …………10分

    又

    故存在正整数M，使得对一切M的最小值为2…………12分

       （2）解法二：，

    令，         …………8分

    由，

    函数…………10分

    对于

    故存在正整数M，使得对一切恒成立，M的最小值为2…………12

    21．解：  1）设椭圆的焦距为2c,因为，所以有，故有。从而椭圆C的方程可化为：      ①                     ………2分

    易知右焦点F的坐标为（），

    据题意有AB所在的直线方程为：   ②                     ………3分

    由①，②有：         ③

    设，弦AB的中点，由③及韦达定理有：

     

    所以，即为所求。                                    ………5分

    2）显然与可作为平面向量的一组基底，由平面向量基本定理，对于这一平面内的向量，有且只有一对实数，使得等式成立。设，由1）中各点的坐标有：

    ，所以

    。                                   ………7分

    又点在椭圆C上，所以有整理为。           ④

    由③有：。所以

       ⑤

    又A?B在椭圆上，故有                ⑥

    将⑤，⑥代入④可得：。                                ………11分

    对于椭圆上的每一个点，总存在一对实数，使等式成立，而

    在直角坐标系中，取点P（），设以x轴正半轴为始边，以射线OP为终边的角为，显然 。

    也就是：对于椭圆C上任意一点M ，总存在角（∈R）使等式：＝cos＋sin成立。                                                 ………12分

     

    22.  …1分

    在上无极值点      ……………………………2分

    当时，令,随x的变化情况如下表：

    x

    ＋

    0

    －

    递增

    极大值

    递减

    从上表可以看出，当时，有唯一的极大值点

    （2）解：当时，在处取得极大值

    此极大值也是最大值。

    要使恒成立，只需

    的取值范围是     …………………………………………………8分

    （3）证明：令p=1，由（2）知:

            …………………………………………………………10分

             ……………………………………………14分


    同步练习册答案