
19.解:
连接BD交AC于O,则BD⊥AC,
连接A1O
在△AA1O中,AA1=2,AO=1,
∠A1AO=60°
∴A1O2=AA12+AO2-2AA1?Aocos60°=3
∴AO2+A1O2=A12
∴A1O⊥AO,由于平面AA1C1C⊥
平面ABCD,
所以A1O⊥底面ABCD
∴以OB、OC、OA1所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系,则A(0,-1,0),B( ,0,0),C(0,1,0),D(-
,0,0),C(0,1,0),D(- ,0,0),A1(0,0,
,0,0),A1(0,0, )
)
……………………2分
(Ⅰ)由于

则
∴BD⊥AA1……………………4分
(Ⅱ)由于OB⊥平面AA1C1C
∴平面AA1C1C的法向量
设 ⊥平面AA1D
⊥平面AA1D
则
得到 ……………………6分
……………………6分

所以二面角D―A1A―C的平面角的余弦值是 ……………………8分
……………………8分
(Ⅲ)假设在直线CC1上存在点P,使BP//平面DA1C1
设
则
得 ……………………9分
……………………9分
设
则 设
设
得到 ……………………10分
……………………10分
又因为 平面DA1C1
平面DA1C1
则 ?
?
即点P在C1C的延长线上且使C1C=CP……………………12分
法二:在A1作A1O⊥AC于点O,由于平面AA1C1C⊥平面
ABCD,由面面垂直的性质定理知,A1O⊥平面ABCD,
又底面为菱形,所以AC⊥BD

……………………4分 (Ⅱ)在△AA1O中,A1A=2,∠A1AO=60° ∴AO=AA1?cos60°=1 所以O是AC的中点,由于底面ABCD为菱形,所以 O也是BD中点 由(Ⅰ)可知DO⊥平面AA1C 过O作OE⊥AA1于E点,连接OE,则AA1⊥DE 则∠DEO为二面角D―AA1―C的平面角 ……………………6分 在菱形ABCD中,AB=2,∠ABC=60° ∴AC=AB=BC=2 ∴AO=1,DO= 在Rt△AEO中,OE=OA?sin∠EAO= DE= ∴cos∠DEO= ∴二面角D―A1A―C的平面角的余弦值是 ……………………8分 ……………………8分 (Ⅲ)存在这样的点P 连接B1C,因为A1B1 AB AB DC DC ∴四边形A1B1CD为平行四边形。 ∴A1D//B1C 在C1C的延长线上取点P,使C1C=CP,连接BP……………………10分 因B1B CC1,……………………12分 CC1,……………………12分 ∴BB1 CP CP ∴四边形BB1CP为平行四边形 则BP//B1C ∴BP//A1D ∴BP//平面DA1C1 20.解: (Ⅰ) 令 ……………………2分 ……………………2分 当 是增函数 是增函数 当 是减函数……………………4分 是减函数……………………4分 ∴ ……………………6分 ……………………6分 (Ⅲ)(i)当 时, 时, ,由(Ⅰ)知 ,由(Ⅰ)知 上是增函数,在 上是增函数,在 上是减函数 上是减函数  ……………………7分 ……………………7分
又当 时, 时, 所以 所以 的图象在 的图象在 上有公共点,等价于 上有公共点,等价于 …………8分 …………8分 解得 …………………9分 …………………9分 (ii)当 时, 时, 上是增函数, 上是增函数, ∴ 所以原问题等价于 又 ∴无解………………11分
| |

![]() B.
B.![]() C.
C.![]() D.不存在
D.不存在![]()
![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]() ( )
( )![]() B.
B.![]() C.
C.![]() D.
D.![]()
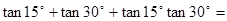 (
)
(
)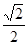 B.1 C.
B.1 C. D.
D.
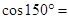 ( )
( ) B.
B.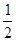 C.
C. D.
D.