
题目列表(包括答案和解析)
(本小题满分12分)
如图,已知在坐标平面xOy内,M、N是x轴上关于原点O对称的两点,P是上半平面内一点,△PMN的面积为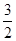 ,点A的坐标为(1+
,点A的坐标为(1+ ),
), 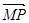 =m·
=m·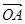 (m为常数),
(m为常数),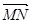
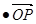
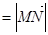
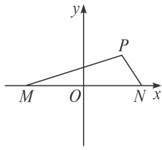
(1)求以M、N为焦点且过点P的椭圆方程;
(2)过点B(-1,0)的直线l交椭圆于C、D两点,交直线x=-4于点E,点B、E分 的比分别为λ1、λ2,求λ1+λ2的值。
的比分别为λ1、λ2,求λ1+λ2的值。
(本小题满分12分)
如图,A、B分别是椭圆 的公共左右顶点,P、Q分别位于椭圆和双曲线上且不同于A、B的两点,设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4且k1+k2+k3+k4=0。
的公共左右顶点,P、Q分别位于椭圆和双曲线上且不同于A、B的两点,设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4且k1+k2+k3+k4=0。
(1)求证:O、P、Q三点共线;(O为坐标原点)
(2)设F1、F2分别是椭圆和双曲线的右焦点,已知PF1//QF2,求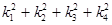 的值。
的值。

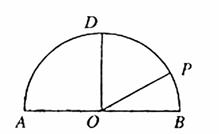
(本小题满分12分)如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)设过点D的直线l与曲线C相交于不同的两点E、F,求直线l斜率的取值范围.

(本小题满分12分)如图,已知M是函数![]() 图像C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A、B,O是坐标原点,求
图像C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A、B,O是坐标原点,求![]() 面积的最小值.
面积的最小值.
(本小题满分12分)如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)设过点D的直线l与曲线C相交于不同的两点E、F,求直线l斜率的取值范围.
一、选择题(每小题5分,共12小题,满分60分)
|