
题目列表(包括答案和解析)
C.选修4-4:坐标系与参数方程
在极坐标系下,已知圆O: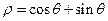 和直线
和直线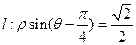 ,
,
(1)求圆O和直线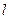 的直角坐标方程;(2)当
的直角坐标方程;(2)当 时,求直线
时,求直线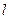 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
D.选修4-5:不等式证明选讲
对于任意实数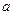
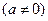 和
和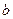 ,不等式
,不等式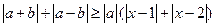 恒成立,试求实数
恒成立,试求实数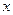 的取值范围.
的取值范围.
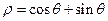 和直线
和直线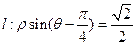 ,
,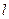 的直角坐标方程;(2)当
的直角坐标方程;(2)当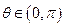 时,求直线
时,求直线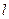 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.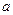
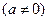 和
和 ,不等式
,不等式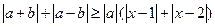 恒成立,试求实数
恒成立,试求实数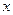 的取值范围.
的取值范围.C
[解析] 由基本不等式,得ab≤![]() =
=![]() =
=![]() -ab,所以ab≤
-ab,所以ab≤![]() ,故B错;
,故B错;![]() +
+![]() =
=![]() =
=![]() ≥4,故A错;由基本不等式得
≥4,故A错;由基本不等式得![]() ≤
≤![]() =
=![]() ,即
,即![]() +
+![]() ≤
≤![]() ,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×
,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =
=![]() ,故D错.故选C.
,故D错.故选C.
.定义域为R的函数 满足
满足 ,且当
,且当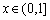 时,
时, ,则当
,则当 时,
时,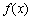 的最小值为( )
的最小值为( )
(A) (B)
(B)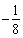 (C)
(C)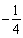 (D)
(D)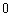
.过点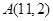 作圆
作圆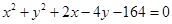 的弦,其中弦长为整数的共有 ( )
的弦,其中弦长为整数的共有 ( )
A.16条 B. 17条 C. 32条 D. 34条
一、选择题:(本大题12个小题,每小题5分,共60分)
1-6 ACBDCB 7-12 ABDADA
二、填空题:(本大题4个小题,每小题4分,共16分)
13.. 14.(-,). 15. 或
或 . 16.7.
. 16.7.
三、解答题:(本大题6个小题,共74分)
17.(12分)
解:
 ,
,
即 ,又6a∈(0,),∴
,又6a∈(0,),∴ ,即
,即 .
.
∴(-)sin4α=
 .
.
变式题:已知(1+tan2α)(1+tan25°)=2,α∈(0, ),求(-)×sin4α的值.
命题意图:本题主要考查三角函数的恒等变形.包含了和差角、倍角的运算,已知三角函数值求角,诱导公式,辅助角公式,要求学生对三角函数的变形方向有综合的理解.
18.(12分)
(Ⅰ)证明:分别取AB,A¢B¢的中点D,D¢,连CD,PD¢,
∵O为△ABC的中心,G为△PA¢B¢的重心,
∴O∈CD,G∈PD¢,且CO∶OD=PG:GD¢=2∶1.
∵AA¢B¢B为□,AD=DB,A¢D¢=D¢B¢,∴DD¢∥AA¢,
又∵AA¢∥CC¢,∴DD¢∥CC¢,即DD¢∥CP.
又CO∶OD=PG∶GD¢=2∶1,∴OG∥DD¢,
∵OG(/平面AA¢B¢B,DD¢Ì平面AA¢B¢B.
∴OG∥平面AA¢B¢B.
(Ⅱ)证明一:当l=时,不妨设AA¢=2,AC=2,由点A¢在平面ABC上的射影为△ABC的中心,连AO并延长交BC于点E,则E为BC的中点,取B¢C¢的中点E¢,连EE¢,AA¢∥EE¢∥CC¢.∵A¢O^平面ABC,∴A¢O^BC.∵O为△ABC中心,∴AE^BC.∴BC^平面AA¢E¢E.设PB¢∩EE¢=Q,∴BC^A¢Q,且E¢Q=CP=AA¢=.∵AO=AC×=.AA¢=2,∴cosÐA¢AO==,∴cosÐA¢E¢E=.在△A¢E¢Q中,A¢E¢=,E¢Q=,
cosÐA¢E¢E=,∴A¢Q2=A¢E¢2+E¢Q2-
∴A¢Q^QE¢,∵QE¢与BC相交,∴A¢Q^平面BB¢C¢C,∵A¢QÌ平面A¢B¢P,∴平面A¢B¢P^平面BB¢C¢C.
证明二:当l=时,不妨设AA¢=2,AC=2,
 由点A¢在平面ABC上的射影为△ABC的中心,连AO并延长交BC于点E,则E为BC的中点,取B¢C¢的中点E¢,连EE¢,AA¢∥EE¢∥CC¢.∵AO^平面ABC,∴AO^BC.∵O为△ABC中心,∴AE^BC.∴BC^平面AA¢E¢E.设PB¢∩EE¢=Q,则Q为PB¢中点.
由点A¢在平面ABC上的射影为△ABC的中心,连AO并延长交BC于点E,则E为BC的中点,取B¢C¢的中点E¢,连EE¢,AA¢∥EE¢∥CC¢.∵AO^平面ABC,∴AO^BC.∵O为△ABC中心,∴AE^BC.∴BC^平面AA¢E¢E.设PB¢∩EE¢=Q,则Q为PB¢中点.
∵在□AA¢C¢C中,A¢A=A¢C=2,A¢C¢=2,
∴cosÐA¢C¢P=,
在△A¢C¢P中,A¢C¢=2,C¢P=,cosÐA¢C¢P=,
∴A¢P==2,
∴A¢B¢=A¢P,∵Q为BP中点,连A¢Q,则A¢Q^B¢P,
∵BC^平面AA¢E¢E,∴BC^A¢Q,∴A¢Q^平面BCC¢B¢.
∵A¢QÌ平面A¢B¢P,∴平面A¢B¢P^平面BB¢C¢C.
(Ⅲ)解法一:当l=1时,不妨设AA¢=AC=2,∵点A¢在平面ABC上的射影为△ABC的中心,∴A¢A=A¢B=A¢C.∴△A¢BC为等边三角形,取A¢B中点M,连CM,则CM^A¢B.CM=.过P作PN^A¢B,垂足为N,则((MC与((NP所成的角即为二面角C-A¢B-P的大小.
 在△PA¢B中,∵P为CC¢中点,∴CP=1,A¢P=.∵AA¢在平面ABC上的射影AO,AO^BC,∴AA¢^BC.∵CC¢∥AA¢,∴CC¢^BC.∵BC=2,CP=1,∴BP=.A¢B=2,∴cosÐPA¢B=,∴A¢N=,NP=,∵A¢M=1,∴MN=.
在△PA¢B中,∵P为CC¢中点,∴CP=1,A¢P=.∵AA¢在平面ABC上的射影AO,AO^BC,∴AA¢^BC.∵CC¢∥AA¢,∴CC¢^BC.∵BC=2,CP=1,∴BP=.A¢B=2,∴cosÐPA¢B=,∴A¢N=,NP=,∵A¢M=1,∴MN=.
∵((CP=-((MC+((MN+((NP,
两边平方得,((CP2=((MC2+((MN2+((NP2-2((MC×((NP,
解得((MC×((NP=.∴cos<((MC,((NP>=\s\up8(((MC
=.
∴二面角C-A¢B-P的大小为arccos.
 解法二:当l=1时,不妨设AA¢=AC=2,∵点A¢在平面ABC上的射影为△ABC的中心,∴A¢A=A¢B=A¢C.∴△A¢BC,△A¢BB¢都为等边三角形.
解法二:当l=1时,不妨设AA¢=AC=2,∵点A¢在平面ABC上的射影为△ABC的中心,∴A¢A=A¢B=A¢C.∴△A¢BC,△A¢BB¢都为等边三角形.
取A¢B的中点M,连CM,B¢M,则CM^A¢B,B¢M^A¢B.
∴ÐB¢MC为二面角B¢-A¢B-C的平面角,
在△B¢CM中,B¢M=CM=,B¢C=2,∴cosÐB¢MC=-.
取BB¢的中点R,连PR,A¢R.则平面A¢PR^平面A¢BB¢.
过P作PQ^A¢R,则PQ^平面A¢BB¢.
过P作PN^A¢B于N,连QN,则QN^A¢B.
∴ÐPNQ为二面角B¢-A¢B-P的平面角,
在△A¢PB中,求得PN=,
在△A¢PR中,求得PQ=.∴sinÐPNQ==.
∵二面角C-A¢B-P等于二面角B¢-A¢B-C与二面角B¢-A¢B-P的差,
设二面角C-A¢B-P的大小为q,
则cosq=cos(ÐB¢MC-ÐPNQ)=cosÐB¢MC×cosÐPNQ+sinÐB¢MC×sinÐPNQ
=-×+×=.
∴二面角C-A¢B-P的大小为arccos.
命题意图:在斜棱柱中,通过图形位置的变化,强调立体图形向平面图形转化的能力,充分利用平面图形的性质来证明线面的平行与垂直,考查用向量法求二面角的大小及用分割法来求二面角的大小.
19.(12分)
【猜题理由】本题在函数和导数、以及线性规划的交汇处命题,具有较强的预测性,而且设问的方式具有较大的开放度,情景新颖.
【解答】(1)由题意有f(0)= c=0,fノ(x)=3 x2+2ax+b,且fノ(1)= 3+
又曲线y=f(x)在原点处的切线的斜率k=fノ(0)= b,而直线y=2x+3到它所成的夹角为450,
∴1=tan450= ,解得b=? 3. 代入3+
故f(x)的解析式为f(x)=x3? 3x.
(2)∵对于任意实数α和β有2sinα,2sinβ∈[-2,2].
由fノ(x)=3x2?3=3(x?1) (x+1)可知,f(x)在(-∞,?1]和[1,+∞)上递增;在[-1,1]递减.
又f(?2)= ?2,f(?1)= 2,f(1)= ?2,f(2)= 2,
∴f(x)在[-2,2]上的最大值和最小值分别为?2和2.
∴对于任意实数α和β恒有| f(2sinα)?f(2sinβ)|≤4.
故m≥4,即m的最小值为4.
(3)∵g(x)=x(x3? 3x)+tx2+kx+s= x4+(t?3)x2+kx+s,∴gノ(x)= 4 x3+2(t?3)x+k,
∴要使g(x)在[-3,?2]上递减,而在[-1,0]上递增,且存在x0(x0>1)使得g(x)在[1,x0]上递减,只需在[-3,?2]和[1,x0]上gノ(x)≤0,而在[-1,0]上gノ(x)≥0.
令h(x)= gノ(x),则hノ(x)= 12 x2+2(t?3),当t?3≥0时,hノ(x)在R上恒为非负,此时显然不存在这样的常数t和k,∴t?3<0.
当t?3<0时,g(x)在(-∞,?]和[,+∞)上递增,而在[?,?]上递减.
∴要使h(x)在[-3,?2]和[1,x0]上h(x)≤0,而在[-1,0]上h(x)≥0,只需h(?2)= ?32 ?4 (t?3)+k

即
作出可行域如图所示,由图可知,当直线t+ k= z过A点时z取得最大值5,当直线t+ k= z过B点时z取得最大值?5.
故存在这样的常数t和k,其取值范围为[-5, 5].
20.(12分)
【猜题理由】本题取材于社会热点问题,情景新颖,背景公平,具有较好的教育意义,而且能较好地考查考生灵活地运用所学的概率知识来分析解决实际问题的能力,体现了新课标的理念.
【解答】(1)若该公司投资研发A项目,则:若该公司在2006年研发成功,其经济效益期望为Eξ11=
若该公司在2006年没有研发成功,而另一个公司在2006年研发成功,于是该公司的经济效益期望为Eξ12=?
若该公司在2007年研发成功,其经济效益期望为
Eξ21=
若该公司在2007年没有研发成功,而另一个公司在2007年研发成功,于是该公司的经济效益期望为Eξ22=?
若该公司在2008年研发成功,其经济效益期望为
Eξ31=
若该公司在2008年没有研发成功,而另一个公司在2008年研发成功,于是该公司的经济效益期望为Eξ32=?
若该公司在2009年研发成功,其经济效益期望为
Eξ41=
若该公司在2009年没有研发成功,而另一个公司在2009年研发成功,于是该公司的经济效益期望为Eξ42=?
若该公司在2010年研发成功,其经济效益期望为
Eξ51=
若该公司在2010年没有研发成功,则该公司总要损失
所以该公司投资研发A项目的经济效益期望为Eξ11+
Eξ12+ Eξ21+ Eξ22+ Eξ31+ Eξ32+
Eξ41+ Eξ42+ Eξ51+ Eξ52≈
其投资的期望为
其投资的经济效益期望的平均效率为≈1.723538,平均每年的经济效益期望为≈11.22333万元.
(2)设该公司投资研发B项目的经济效益为η万元,则ξ的可能取值为
∴Eη=
其投资的期望为
其投资的经济效益期望的平均效率为2.3076923,平均每年的经济效益期望为
尽管A项目的投资经济效益期望的平均效率比B项目略低,但总的经济效益期望和平均每年的经济效益期望比B项目高得多,故应建议该公司在2006年投资研发A项目.
21.(12分)
【猜题理由】本题本题在平面向量和解析几何的交汇处命题,重点考查了解析几何的基本思想方法,体现最新《考试大纲》的要“构造有一定的深度和广度的数学问题”高考命题要求.
【解答】(1)设(x,y),∵ +
+ +
+ =0,∴M点是ΔABC的重心,∴M(,).
=0,∴M点是ΔABC的重心,∴M(,).
又| |=|
|=| |且向量
|且向量 与
与 共线,∴N在边AB的中垂线上,∴N(0,).
共线,∴N在边AB的中垂线上,∴N(0,).
而| |=|
|=| |,∴=,即x2? =a2.
|,∴=,即x2? =a2.
(2)设E(x1,y1),F(x2,y2),过点P(0,a)的直线方程为y=kx+a,
代入x2? =a2得 (3?k2)x2?2akx?
∴Δ=
而x1,x2是方程的两根,∴x1+x2=,x1x2=.
∴ ?
? =(x1,y1?a)?(x2,y2?a)= x1x2+kx1?kx2=(1+k2) x1x2==
=(x1,y1?a)?(x2,y2?a)= x1x2+kx1?kx2=(1+k2) x1x2==
故 ?
? 的取值范围为(-∞,
的取值范围为(-∞,
(3) 设Q(x0,y0) (x0>0,x0>0),则x02? =a2,即y02=3(x02?a02).
当QH⊥x轴时,x0=
当QH不垂直x轴时,tan∠QHG=?,tan∠QGH= ,
∴tan2∠QGH= = = = =?= tan∠QHG.
又2∠QGH与∠QHG同在(0,)∪(,π)内,∴2∠QGH=∠QHG.
故存在λ=2,使2∠QGH=∠QHG恒成立.
22.(14分)
【猜题理由】本题以导数为背景,命制出数列与函数、导数、不等式的综合试题,重点考查数列的基本思想方法,综合较强,与高考的压轴题的难度相当,具有较强的预测性.
【解答】(1)∵fノ(x)=2x,∴切线l2k?1的方程为y?x2k?12=2 x2k?1(x?x2k?1),又切线l2k?1过点A2k?2(x2k?2,0),∴0?x2k?12=2 x2k?1(x2k?2?x2k?1),且x2k?1>0,∴x2k?1=2 x2k?2.∴x1=2.
(2)又gノ(x)=( ex) ノ= ex,∴切线l2k的方程为y?e =e
=e (x?x2k),而切线l2k过点A2k?1(x2k?1,0),∴0?e
(x?x2k),而切线l2k过点A2k?1(x2k?1,0),∴0?e = e
= e (x2k?1?x2k),且x2k>0,∴x2k= x2k?1+1. ∴x2=x1+1=3.
(x2k?1?x2k),且x2k>0,∴x2k= x2k?1+1. ∴x2=x1+1=3.
(3)由(1) (1)可知x2k= x2k?1+1 = 2x2k?2+1,即x2k+1= 2(x2k?2+1),∴数列{x2k +1}为等比数列,且首项为4,∴x2k +1=4×2k?1,即x2k =2k+1?1.
而x2k?1=2 x2k?2=2(2k?1)= 2k+1?2,故数列{xn}通项公式为xn=
(4) (理)令Sn= + ++…+= +++…+, ∴Sn= +++…+,
两式相减得Sn= ++++…+? = ? = (1?)?,
∴Sn=1?? =1?.
∴Sn+1? Sn=(1?)?(1? )=>0,∴数列{ Sn}递增.
又当n≥6时,2n+1=2(1+1) n=2(1+C+C+C+C+…+C+C+C+C)>4(1+C+C)>2(n2+n),∴0<<,而=0,∴Sn=1.
令h(x)= 3tx4?4tx3?12tx2+33t?,则hノ(x)= 12t(x3?x2?2x)= 12tx(x+1)(x?2),
∴当t<0时,h(x)在(?∞,?1)和(0,2)上递增,在(?1, 0)和(2,+∞)上递减,此时不存在这样的实数t.
当t>0时,h(x)在(?∞,?1)和(0,2)上递减,在(?1, 0)和(2,+∞)上递增,
∴h(x)在x=?1或x=2处取得极小值,而h(?1)=?5t+33t?,h(2)=?32t+33t?,
∴h(x)min= t?.
∴对于任意的自然数n和任意的实数x不等式恒成立等价于t?≥1,
而t>0,所以有t2?t?6≥0,解得t≥3或t≤?2 (舍).
故存在这样的实数t,其取值范围为t≥3.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com