.files\image175.jpg)
.files\image019.jpg) 19.(本小题满分12分)
19.(本小题满分12分)
.files\image019.jpg) 解法一:
解法一:
.files\image019.jpg) (I)证明
(I)证明
.files\image019.jpg) 如图,连结AC,AC交BD于点G,连结EG。
如图,连结AC,AC交BD于点G,连结EG。
.files\image019.jpg) ∵ 底面ABCD是正方形,
∵ 底面ABCD是正方形,
.files\image019.jpg) ∴ G为AC的中点.
∴ G为AC的中点.
.files\image019.jpg) 又E为PC的中点,
又E为PC的中点,
.files\image019.jpg) ∴EG//PA。
∴EG//PA。
.files\image019.jpg) ∵EG
∵EG.files\image179.gif) 平面EDB,PA
平面EDB,PA.files\image181.gif) 平面EDB,
平面EDB,
.files\image019.jpg) ∴PA//平面EDB
………………4分
∴PA//平面EDB
………………4分
.files\image019.jpg) (II)证明:
(II)证明:
.files\image019.jpg) ∵ PD⊥底面ABCD,∴PD⊥BC,PD⊥DC,PD⊥DB
∵ PD⊥底面ABCD,∴PD⊥BC,PD⊥DC,PD⊥DB
.files\image019.jpg) 又∵BC⊥DC,PD∩DC=D,
又∵BC⊥DC,PD∩DC=D,
.files\image019.jpg) ∴BC⊥平面PDC。
∴BC⊥平面PDC。
.files\image019.jpg) ∴PC是PB在平面PDC内的射影。
∴PC是PB在平面PDC内的射影。
.files\image019.jpg) ∵PD⊥DC,PD=DC,点E是PC的中点,
∵PD⊥DC,PD=DC,点E是PC的中点,
.files\image019.jpg) ∴DE⊥PC。
∴DE⊥PC。
.files\image019.jpg) 由三垂线定理知,DE⊥PB。
由三垂线定理知,DE⊥PB。
.files\image019.jpg) ∵DE⊥PB,EF⊥PB,DE∩EF=E,
∵DE⊥PB,EF⊥PB,DE∩EF=E,
.files\image019.jpg) ∴PB⊥平面EFD。
…………………………8分
∴PB⊥平面EFD。
…………………………8分
.files\image019.jpg) (III)解:
(III)解:
.files\image019.jpg) ∵PB⊥平面EFD,
∵PB⊥平面EFD,
.files\image019.jpg) ∴PB⊥FD。
∴PB⊥FD。
.files\image019.jpg) 又∵EF⊥PB,FD∩EF=F,
又∵EF⊥PB,FD∩EF=F,
.files\image019.jpg) ∴∠EFD就是二面角C―PB―D的平面角。………………10分
∴∠EFD就是二面角C―PB―D的平面角。………………10分
.files\image019.jpg) ∵PD=DC=BC=2,
∵PD=DC=BC=2,
.files\image019.jpg) ∴PC=DB=
∴PC=DB=.files\image183.gif)
.files\image019.jpg) ∵PD⊥DB,
∵PD⊥DB,
.files\image019.jpg)
.files\image185.gif)
由(II)知:DE⊥PC,DE⊥PB,PC∩PB=P,
∴DE⊥平面PBC。
∵EF.files\image179.gif) 平面PBC,
平面PBC,
∴DE⊥EF。
.files\image188.gif)
∴∠EFD=60°。
故所求二面角C―PB―D的大小为60°。 ………………12分
解法二:
如图,以点D为坐标原点,DA、DC、DP所在直线分别为x轴、y轴、z轴,
建立空间直角坐标系,得以下各点坐标:D(0,0,0),A(2,0,0),B(2,2,0),
C(0,2,0),P(0,0,2) ………………1分
(I)证明:
连结AC,AC交BD于点G,连结EG。
∵ 底面ABCD是正方形,
∴ G为AC的中点.G点坐标为(1,1,0)。
.files\image190.jpg)
.files\image192.gif)
∴PA//平面EDB ………………4分 (II)证明: .files\image194.gif)
(III)解: ∵PB⊥平面EFD, ∴PB⊥FD。 又∵EF⊥PB,FD∩EF=F, ∴∠EFD就是二面角C―PB―D的平面角。………………10分 .files\image196.gif)
∴∠EFD=60°。 故所求二面角C―PB―D的大小为60°。 ………………12分 20.(本小题满分12分) (I)解: 设 “从甲盒内取出的2个球均为黑球”为事件.files\image198.gif) ,“从乙盒内取出的2个球均为黑球”为事件 ,“从乙盒内取出的2个球均为黑球”为事件.files\image200.gif) .由于事件 .由于事件.files\image202.gif) 相互独立,所以取出的4个球均为黑球的概率为 相互独立,所以取出的4个球均为黑球的概率为 .files\image204.gif) ………………2分 ………………2分
依题设.files\image206.gif) , , .files\image208.gif)
故乙盒内红球的个数为2。 ……………………5分 (II)解: .files\image210.gif) 由(I)知 由(I)知 .files\image212.gif)
ξ的分布列为 ξ 0 1 2 3 P .files\image214.gif)
.files\image216.gif)
.files\image218.gif)
.files\image220.gif)
………………10分 .files\image222.gif) ………………12分 ………………12分
21.(本小题满分12分) (I)解:由题意设双曲线S的方程为.files\image224.gif) ………………2分 ………………2分 c为它的半焦距, .files\image226.gif)
(II)解: .files\image228.gif)
22.(本小题满分12分) (I)解: .files\image230.gif)
.files\image232.gif) (III)解: .files\image234.gif)
(III)解: .files\image236.gif)
.files\image238.gif) w.w.w.k.s.5.u.c.o.m w.w.w.k.s.5.u.c.o.m
www.ks5u.com
| |

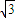 πa3,12πa2
πa3,12πa2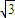 πa3,3πa2
πa3,3πa2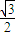 4πa3,12πa2
4πa3,12πa2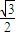 4πa3,3πa2
4πa3,3πa2 πa3,12πa2
πa3,12πa2 πa3,3πa2
πa3,3πa2 4πa3,12πa2
4πa3,12πa2 4πa3,3πa2
4πa3,3πa2.files\image019.jpg)
.files\image019.jpg) 一、选择题:本大题共12小题,每小题5分,共60分。
一、选择题:本大题共12小题,每小题5分,共60分。.files\image019.jpg) 1―5 DABBA 6―10 DDCCB 11―12 AC
1―5 DABBA 6―10 DDCCB 11―12 AC.files\image019.jpg) 二、填空题:本大题共4小题,每小题5分,共20分。
二、填空题:本大题共4小题,每小题5分,共20分。.files\image019.jpg) 13.
13..files\image149.gif) 14.
14..files\image151.gif) 15.
15..files\image153.gif) 16.②④
16.②④.files\image019.jpg) 三、解答题:本大题共6小题,满分70分。
三、解答题:本大题共6小题,满分70分。.files\image019.jpg) 17.(本小题满分10分)
17.(本小题满分10分).files\image019.jpg) (I)解:
(I)解:.files\image019.jpg)
.files\image155.gif) 时,
时,.files\image019.jpg)
.files\image157.gif) ………………2分
………………2分.files\image019.jpg)
.files\image159.gif) ………………4分
………………4分.files\image019.jpg)
.files\image161.gif) ,
, .files\image019.jpg)
.files\image163.gif) ………………5分
………………5分.files\image019.jpg) (II)解:
(II)解:.files\image019.jpg)
.files\image165.gif)
.files\image019.jpg) 18.(本小题满分12分)
18.(本小题满分12分).files\image019.jpg) (I)解:
(I)解:.files\image019.jpg)
.files\image167.gif)
.files\image019.jpg)
.files\image169.gif)
.files\image019.jpg) (II)解:
(II)解:.files\image019.jpg) 由(I)知:
由(I)知:.files\image171.gif)
.files\image019.jpg)
.files\image173.gif)
.files\image019.jpg) (III)解:
(III)解:.files\image019.jpg)