
题目列表(包括答案和解析)
已知圆
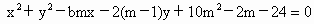 (m∈R)
(m∈R)
(1)求证:不论m为何值,圆心在同一直线l上.
(2)
与l平行的直线中,哪些与圆相交、相切、相离.(3)
求证:任何一条平行于直线l且与圆相交的直线被圆截得的弦长相等.已知圆
 (mÎ
R),
(mÎ
R),
(1)
求证不论m为何值,圆心在同一直线l上.(2)
与l平行的直线中,哪些与圆相交、相切、相离.(3)
求证:任何一条平行l且与圆相交的直线被圆截得的弦长相等.已知圆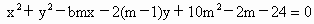 (m∈R)
(m∈R)
(1)求证:不论m为何值,圆心在同一直线l上.
(2)与l平行的直线中,哪些与圆相交、相切、相离.
(3)求证:任何一条平行于直线l且与圆相交的直线被圆截得的弦长相等.
已知圆 (mÎ
R),
(mÎ
R),
(1)求证不论m为何值,圆心在同一直线l上.
(2)与l平行的直线中,哪些与圆相交、相切、相离.
(3)求证:任何一条平行l且与圆相交的直线被圆截得的弦长相等.
.files\image032.jpg)
.files\image032.jpg) 一、选择题:本大题共12小题,每小题5分,共60分。
一、选择题:本大题共12小题,每小题5分,共60分。
.files\image032.jpg) 1―5 ADBBA 6―10 DDCBC 11―12 CA
1―5 ADBBA 6―10 DDCBC 11―12 CA
.files\image032.jpg) 二、填空题:本大题共4小题,每小题5分,共20分。
二、填空题:本大题共4小题,每小题5分,共20分。
.files\image032.jpg) 13.300 14.
13.300 14..files\image150.gif) 15.
15..files\image152.gif) 16.②④
16.②④
.files\image032.jpg) 三、解答题:本大题共6小题,满分70分。
三、解答题:本大题共6小题,满分70分。
.files\image032.jpg) 17.(本小题满分10分)
17.(本小题满分10分)
.files\image032.jpg) (I)解:
(I)解:
.files\image032.jpg)
.files\image154.gif) 时,
时,
.files\image032.jpg)
.files\image156.gif) ………………2分
………………2分
.files\image032.jpg)
.files\image158.gif) ………………4分
………………4分
.files\image032.jpg)
.files\image160.gif) ,
,
.files\image032.jpg)
.files\image162.gif) ………………5分
………………5分
.files\image032.jpg) (II)解:
(II)解:
.files\image032.jpg)
.files\image164.gif)
.files\image032.jpg) 18.(本小题满分12分)
18.(本小题满分12分)
.files\image032.jpg) (I)解:
(I)解:
.files\image032.jpg)
.files\image166.gif)
.files\image032.jpg)
.files\image168.gif)
.files\image032.jpg) (II)解:
(II)解:
.files\image032.jpg) 由(I)知:
由(I)知:.files\image170.gif)
.files\image032.jpg)
.files\image172.gif)
.files\image032.jpg) (III)解:
(III)解:
.files\image032.jpg)
|