
∴AB//平面DEF. …………3 分
(2)过D点作DG⊥AC 于G,连结BG,
∵AD⊥CD, BD⊥CD,
∴∠ADB 是二面角A―CD―B 的平面角.
∴∠ADB = 90°, 即BD⊥AD.
∴BD⊥平面ADC.
∴BD⊥AC.
∴AC⊥平面BGD.
∴BG⊥AC .
∴∠BGD 是二面角B―AC―D 的平面角. 5 分
在Rt△ADC 中,AD = a,DC =  a,AC = 2a,
a,AC = 2a,
∴
在Rt

即二面角B―AC―D的大小为 ……………………8分
……………………8分
(2)∵AB//EF,
∴∠DEF(或其补角)是异面直线AB 与DE 所成的角. ………………9 分
∵AB = ,
,
∴EF=  ak .
ak .
又DC =  a,CE = kCA
= 2ak,
a,CE = kCA
= 2ak,
∴DF= DE =
 ………………4分
………………4分
∴cos∠DEF= ………………11分
………………11分
∴
 …………………………12分
…………………………12分
19.解:(1)依题意建立数学模型,设第n 次服药后,药在体内的残留量为an(毫克)
a1 = 220,a2 =220×1.4 ……………………2 分
a4 = 220 + a2 (1-0.6) = 343.2 ……………………5 分
(2)由an = 220 + 0.4an―1 (n≥2 ),
可得
所以( )是一个等比数列,
)是一个等比数列,

 不会产生副作用……………………13分
不会产生副作用……………………13分
20.解:(1)由条件知:
 ……………………2分
……………………2分
得 b=1,
b=1,
∴椭圆C的方程为: ……………………4分
……………………4分
(2)依条件有: ………………5分
………………5分
由 …………7分
…………7分
 ,
,
则 ………………7分
………………7分
又



由
 …………………………9分
…………………………9分
由弦长公式得
由 得
得


=
又
 …………………………13分
…………………………13分
21.解:(1)当
令

 上单调递增,
上单调递增,
 ……………………5分
……………………5分
(2) (1),
(1),
需求一个 ,使(1)成立,只要求出
,使(1)成立,只要求出
 的最小值,
的最小值,
满足
 上↓
上↓
在 ↑,
↑,

只需证明 内成立即可,
内成立即可,
令
为增函数
 ,故存在与a有关的正常数
,故存在与a有关的正常数 使(1)成立。13分
使(1)成立。13分

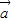 与
与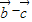 都是非零向量,则“
都是非零向量,则“ ”是“
”是“ ”的充要条件;②已知等腰△ABC的腰为底的2倍,则顶角A的正切值是
”的充要条件;②已知等腰△ABC的腰为底的2倍,则顶角A的正切值是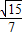 ;③在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为(0,-1);④设
;③在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为(0,-1);④设 ,
,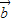 ,
, 为同一平面内具有相同起点的任意三个非零向量,且满足
为同一平面内具有相同起点的任意三个非零向量,且满足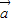 与
与 不共线,
不共线, ⊥
⊥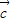 ,|
,| |=|
|=|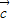 |,则|
|,则| •
•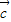 |的值一定等于以
|的值一定等于以 ,
,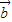 为邻边的平行四边形的面积.其中正确命题的序号是 .(写出全部正确结论的序号)
为邻边的平行四边形的面积.其中正确命题的序号是 .(写出全部正确结论的序号) 10.
10. 11.91
12.②④
11.91
12.②④ 14.(i)
14.(i) (2分) (ii)
(2分) (ii) (3分)
(3分) (3分); (ii)
(3分); (ii) (2分)
(2分)